What do you know about Squares?
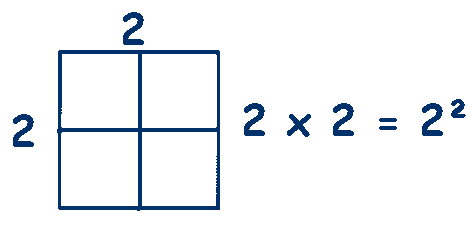 Let the set consisting of the squares of the positive integers be called
u
;
thus
u
is the set 1,4,9, .... If a certain operation on one or more members
of the set always yields a member of the set, we say that the set is closed
under that operation. Then
u
is closed under:
Let the set consisting of the squares of the positive integers be called
u
;
thus
u
is the set 1,4,9, .... If a certain operation on one or more members
of the set always yields a member of the set, we say that the set is closed
under that operation. Then
u
is closed under:
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The set consists of all possible positive perfect squares.Let an integer be a .Then it's square will be a 2 and let a second integer be b .Then it's square will be b 2 .Both of these are integers which are present in the set u .Then: a 2 × b 2 = a × a × b × b = ( a × b ) × ( a × b ) = a b × a b = ( a b ) 2 And as a and b are integers so a b is an integer so ( a b ) 2 is an integer which is present in the set.So the set u is closed under M u l t i p l i c a t i o n