Another proof without words!
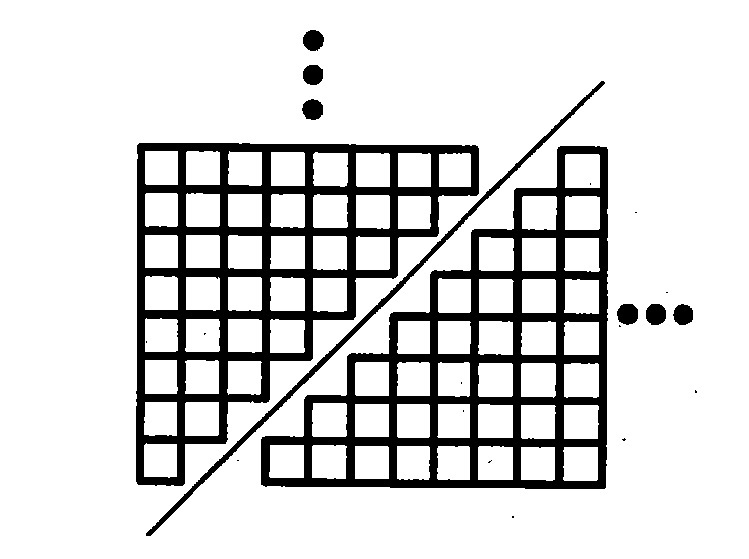 What does the image demonstrate?
What does the image demonstrate?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
It's very clear to figure out that these two portions individually expresses 1+2+3+4+5+6+7+8 which is a sum of algebraic expression with formula
n ( n + 1 ) / 2
Concrete model is (8*9)/2, n=8, so .5(n)(n+1)
triangle problem and its answer 1/2(n+1)
It's nothing but a series of nth term natural number............1+2+3+......+n..........so the sum should be: n(n+1)/2............
these proof demonstrates sum of polymise i for i =1 to i=n So wed have 1 +2+3+.....n= n(n+1)/2
Triangular numbers {n(n+1)}/2 are half of oblong numbers {n(n+1)}
These proof demonstrates the Gauss method to solve 1 + 2 + 3 + 4 + . . . + 1 0 0 . The formula is 2 n ( n + 1 ) .
If you use this formula as a function, when n is one of the natural numbers you get the Triangular Numbers.