What exactly is it?
For any real number x, let [ x ] denote the largest integer less than or equal to x let f be a real valued function defined on the interval [ − 1 0 , 1 0 ] by
f ( x ) f ( x ) = = x − [ x ] , if f [ x ] is odd 1 + [ x ] − x , if f [ x ] is even
Then find the value of 1 0 π 2 ∫ − 1 0 1 0 [ f ( x ) cos ( π x ) ] d x is?
To try more such problems click here .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Thanks for the solution!
Can you check the definition of f ( x ) ? On the conditionals, I think you want just [ x ] instead of f [ x ] right?
Note that when calculating I 2 , after you defined t = x − 1 , you did not change the limits of integration. It should be ∫ 0 1 instead of ∫ 1 2 .
Log in to reply
yeah the intervals was a typing error, and the definition is correct after you made the correction. Now, I guess there is no more correction needed.
This is a previous year JEE problem . A good one . :)
@Calvin Lin and @Eilon Lavi here is the solution,
f ( x ) f ( x ) = = x − [ x ] , if f [ x ] is odd 1 + [ x ] − x , if f [ x ] is even
⇒ f ( x ) = { x − 1 , 1 ≤ x < 2 1 − x , 0 ≤ x < 1 }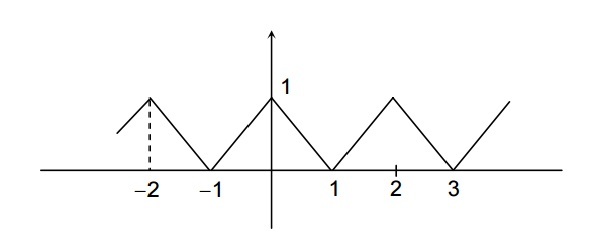
f ( x ) i s p e r i o d i c w i t h p e r i o d 2
∴ I = ∫ − 1 0 1 0 f ( x ) . c o s π x d x
I = 2 ∫ 0 1 0 f ( x ) . c o s π x d x = 2 × 5 ∫ 0 2 f ( x ) . c o s π x d x
= 1 0 [ ∫ 0 1 ( 1 − x ) . c o s π x d x + ∫ 1 2 ( x − 1 ) . c o s π x d x ] = 1 0 ( I 1 + I 2 )
N o w , I 2 = ∫ 1 2 ( x − 1 ) c o s π x d x p u t x − 1 = t
I 2 = − ∫ 0 1 t . c o s π t d t = − ∫ 0 1 x . c o s π x d x
A l s o , I 1 = ∫ 0 1 ( 1 − x ) c o s π x d x = − ∫ 0 1 x . c o s π x d x
⇒ I = 1 0 [ − 2 ∫ 0 1 x . c o s π x d x ]
I = − 2 0 [ x π s i n π x + π 2 c o s π x ] 0 1
I = − 2 0 [ − π 2 1 − π 2 1 ]
⇒ 1 0 π 2 I = 4