What fraction of a regular tetrahedron is closer to center than any surface?
This problem's question is its title. Since the volumes of both the regular tetrahedron and the interior closer space scale with the cube of the edge the fraction remains the same regardless of the chosen edge length. The answer is in parts per billion rounded to an integer, i.e., .
Entire tetrahedron:
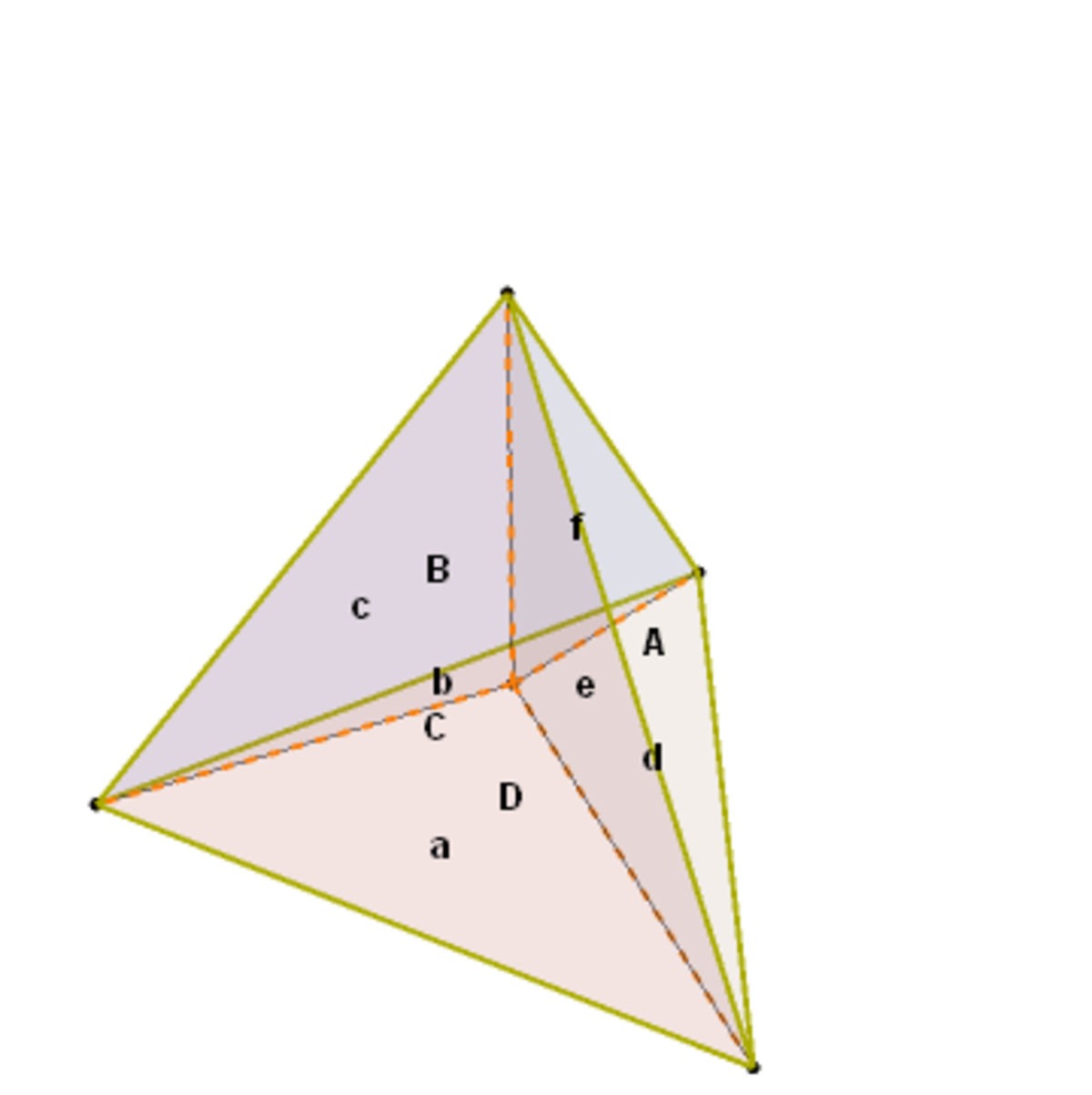
Lower face tetrahedron:
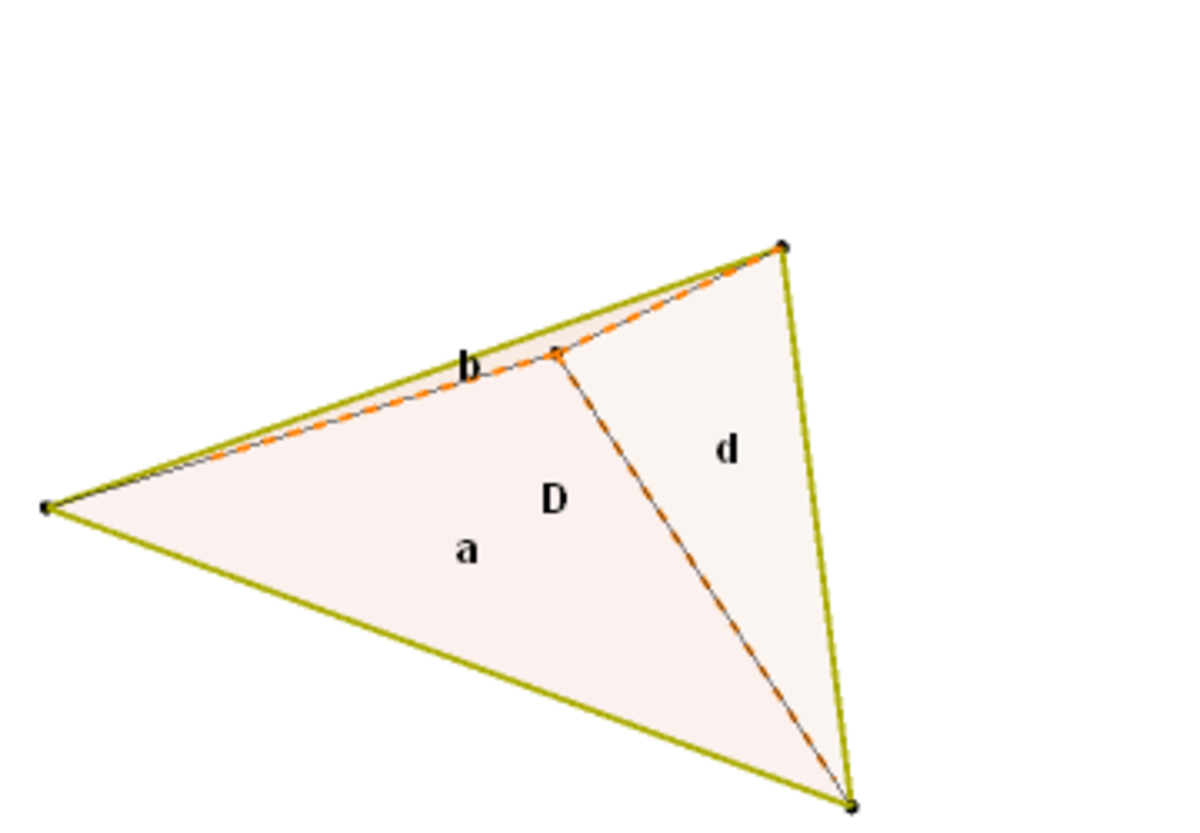
Left fron edge tetrahedron
The volume ratio remains the same for all three shapes
The answer is 59753036.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Round ⎣ ⎡ 1 0 9 1 4 4 2 1 1 8 4 3 2 2 6 3 π − 2 5 ⎦ ⎤ → 5 9 7 5 3 0 3 6
Oh, you say, a little more explanation would be helpful. OK.
The left front irregular tetrahedron is 2 4 1 the volume of the original regular tetrahedron. Why that is true is left as an exercise for the reader.
The interior (i.e., closer to center) shape in the lower face tetrahedron is a section of a paralleloid of revolution with its vertex midway between the center of the original regular tetrahedron and the center of the face of the original regular tetrahedron directly below. Again, why that is true is left as an exercise for the reader. With added coordinates, here is the lower left edge tetrahedron again:
Oh, you say, a little more explanation would be helpful. OK.
Solving the following for z gives 4 6 2 4 x 2 + 2 4 y 2 − 1 , which gives the paralleloid's equation: EuclideanDistance [ { x , y , z } , { x , y , − 2 6 1 } ] = EuclideanDistance [ { x , y , z } , { 0 , 0 , 0 } ]
Solving the following, which is the intersection between the top triangular face of the lower left edge tetrahedron and the paralleloid described above for x , y , z in terms of x gives, which gives the path along the front edge of the interior shape: { x , 1 2 1 ( 3 − 3 1 − 1 6 x 2 ) , 2 4 1 ( 6 − 3 2 − 3 2 x 2 ) } if − 8 1 ≤ x ≤ 0
The integral: ∫ − 8 1 0 ∫ 1 2 1 ( 3 − 3 1 − 1 6 x 2 ) 3 x ∫ 4 6 2 4 x 2 + 2 4 y 2 − 1 2 y d z d y d x
Oh, you say, a little more explanation would be helpful. OK.
Doing the integral in stages: i n t 4 6 2 4 x 2 + 2 4 y 2 − 1 2 y 1 d z → 2 y − 4 6 2 4 x 2 + 2 4 y 2 − 1 ∫ 1 2 1 ( 3 − 3 1 − 1 6 x 2 ) 3 x ( 2 y − 4 6 2 4 x 2 + 2 4 y 2 − 1 ) d y → − 1 4 4 2 ( 4 x − 1 ) ( 3 3 − 4 8 x 2 + 4 x ( 3 3 − 4 8 x 2 + 2 0 x − 1 ) − 4 ) ∫ − 8 1 0 − 1 4 4 2 ( 4 x − 1 ) ( 3 3 − 4 8 x 2 + 4 x ( 3 3 − 4 8 x 2 + 2 0 x − 1 ) − 4 ) d x → 1 8 4 3 2 2 6 3 π − 2 5
Oh, you say, a little more explanation would be helpful. Sorry, this time it is left for an exercise for the reader.