What Fraction of the Circle is Shaded?
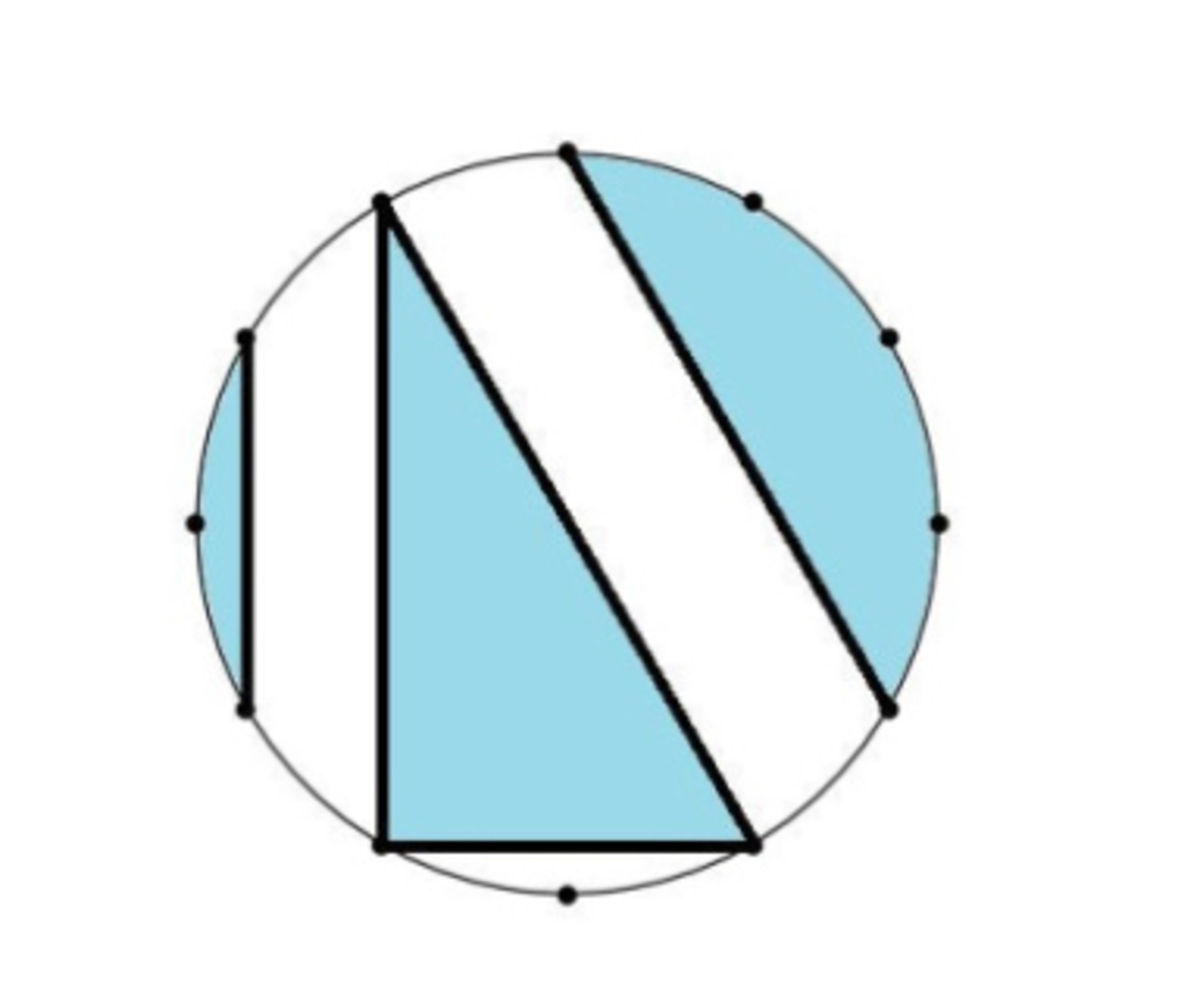
What fraction of the circle is shaded? The twelve points on the circle are equally spaced.
The answer is 0.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
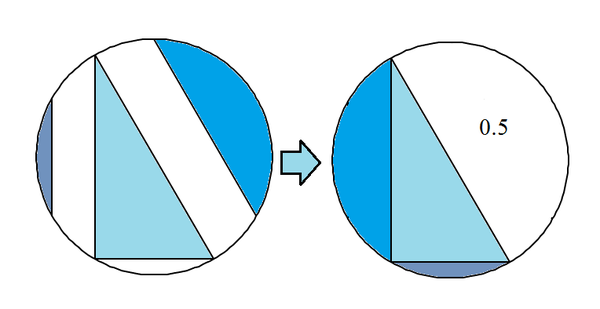
Wow! a simple proof without words. Great one, upvoted!
By moving pieces, it is easy to observe that the fraction of the shaded part is 2 1
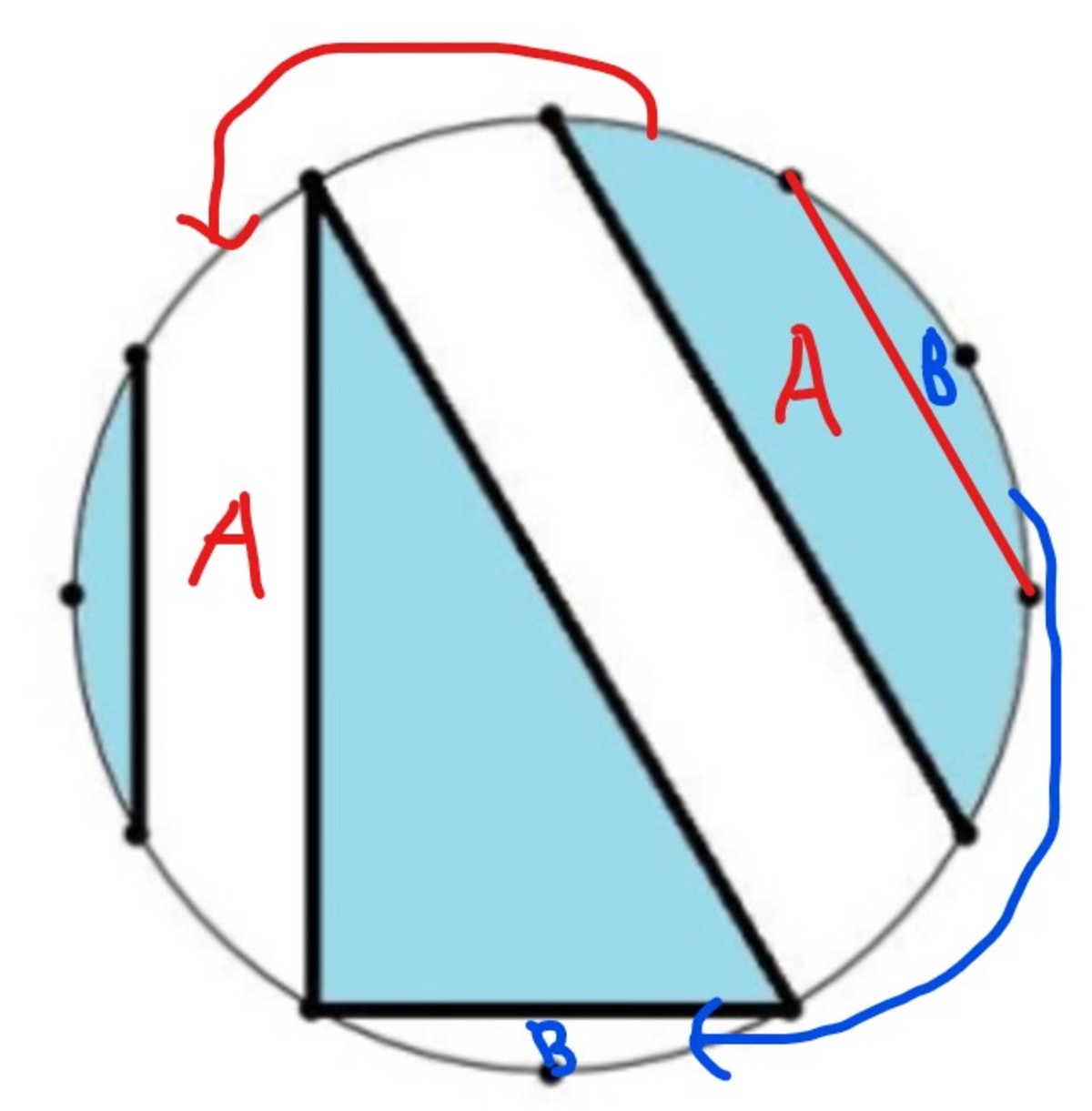
Let the center of the circle be O , radius of the circle be r and the end points of the leftmost shaded region be A and B respectively. Then the area of this region is the difference between the area of the circular sector O A B and the area of the triangle O A B . Since the central angle of this region is 3 π , therefore the area of this region is 2 1 r 2 × 3 π − 4 3 r 2 = r 2 ( 6 π − 4 3 ) . Base of the right angled triangle is 2 r sin 6 π = r and it's height is 2 r sin 3 π = r 3 . So it's area is r 2 2 3 . The angle subtended by the top right shaded region at the centre of the circle is 3 2 π . Therefore it's area is r 2 ( 3 π − 4 3 ) . Therefore total area of the shaded region is r 2 ( 6 π − 4 3 + 2 3 + 3 π − 4 3 ) = 2 π r 2 . Therefore the required fraction is 2 1 = 0 . 5
Aliter :
Place the leftmost shaded region in the bottom most unshaded region. (This will fit exactly there). Place the top right shaded region in the leftmost position (this will also fit exactly there). Now exactly half of the circle will be shaded (the hypotenuse of the right angled triangle is the diameter of the circle). So the required fraction is 0 . 5
@Alak Bhattacharya , l like your solution but please can you elaborate more on how you got your numbers by adding more explanation so your solution will be clear to all. Thank you again for sharing your solution.
Instead of the manipulations of the pieces as shown in the other explanations, we can "bash it out".
WLOG let r = 1 . We first note that since it is divided into 1 2 pieces, each arc measures 3 0 ∘ . Thus, the leftmost region is the area of the 6 0 ∘ sector subtracted by an equilateral triangle of side length 1 . This has area 6 π − 4 3 . The middle triangle's area could be found by finding it's side lengths, which are 1 and 3 , found using similar triangle constructions. Thus, the area of this is 2 3 . Now, for the rightmost piece, we see the the arc has measure 1 2 0 ∘ , so we split it into two 3 0 ∘ − 6 0 ∘ − 9 0 ∘ triangles, getting 3 π − 4 3 as its area. Thus, the fraction of the circle shaded is π ( 6 π − 4 3 ) + ( 3 π − 4 3 ) + 2 3 = 2 1 .