What goes up sometimes stays there
Accelerometers are commonly found in mobile game devices - they measure the motion of the device which can be used to interact with a game. A simple accelerometer can be constructed by placing a small coin in a hemispherical bowl. If you are not accelerating, the coin rests at the bottom of the bowl. If, however, you are accelerating horizontally the coin will slide up the side until it stops at some height and stays there.
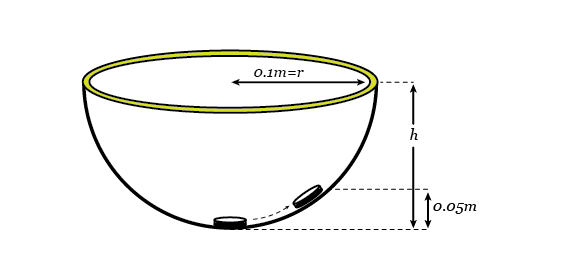
If the bowl has a radius of 0.1 m and the coin comes to rest at a vertical height of 0.05 m above the bottom of the bowl, what is the magnitude of your acceleration in m / s 2 ?
Details and assumptions
- Neglect any friction between the sides of the bowl and the coin.
- The acceleration due to gravity is − 9 . 8 m / s 2 .
The answer is 16.97.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
The coin comes at rest when the net force acting on it is zero. There are three forces acting on the coin: force of gravity, normal force, and force from the acceleration. Let m be the mass of the coin. Then the force of gravity is mg. Since it is given that the coin is at height 0.05m, and the radius of the bowl is 0.1m, then the line of normal force makes a 30 degree angle under a horizontal line. Since gravity and the normal force are the only forces with a y-component, then they cancel out. Hence
Fn = mg/sin30
Similarly, since gravity and the normal force are the only forces with an x-component, then they cancel out. Hence
Fn = ma/cos30
Combining the two equations, we get
a = g cos30/sin30 = 16.974 m/s2
If the coin stays still with respect to you, then the vertical component of the acceleration is zero, while the horizontal component matches your acceleration. The vertical forces on the coin are the force of gravity and the vertical component of the normal force. If θ is the angle between the vertical axis passing through the center of the hemisphere and the line between the coin and the center of the hemisphere, and N is the magnitude of the normal force, then the net vertical force is − m g + N c o s θ = m a y = 0 . N is therefore N = m g / c o s θ . The horizontal component of the normal force generates the horizontal acceleration a of the coin, and so m a x = N s i n θ = m g t a n θ . c o s θ is given by ( 0 . 1 − 0 . 0 5 ) / 0 . 1 = 0 . 5 and so we can solve for a x = 1 6 . 9 7 m / s 2 .
the angle between the line from rest position of coin to the center of the sphere and the line from the spinning coin to the center, k = cos^-1 (.05/.1) = 60 degree. using conical pendulum formula, we have T sin k = ma, and T cos k = mg. Divide the former and the later formula we get tan k = a/g sqrt(3) = a/9.8 a = 16.97m/ss