What happens? Numerical integration problem. 3-4-5 triangle. 3,4&5 mass test masses.
Pure Newtonian gravity used. Special and general relativity issues ignored. This is the entire universe. These are test masses (that is, collisions can not occur by definition).
Three end states are to be considered: it is a closed system (that is, the objects can not escape), a singleton and a pair escape or they escape as three singletons on separated paths. The problem is to decide which case occurs.
As this is a three body problem, the use of numerical integration is strongly suggested.
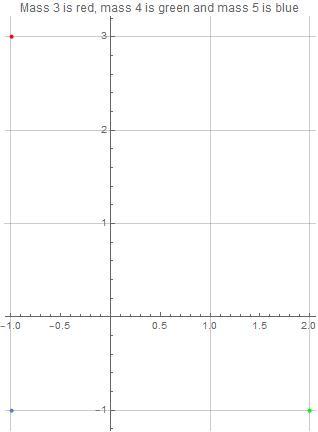
The positions are a 3-4-5 Pythagorean right triangle. The masses are that of the opposite side of the triangle. In the included diagram, the mass=3 object is red, the mass=4 object is green and the mass=5 object is blue. Initially, the objects are stationary at those respective locations.
You may select whatever gravitation constant and time scale you wish as only the qualitative result is needed.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The vertical axis in the graphic is time. The x and y coordinates can be identified by looking at the starting positions.
Even Mathematica had trouble with this numerical integration because of how stiff it is. I used implicit Runge-Kutta to avail the correct answer, which is in the 1967 NASA paper. NASA also had troubles.
Here is a solution from NASA from 1967.