What Happens When Krishna and SG Jump Together?
 On a hot summer evening, two Best Friends
SG
and
Krishna
decide to jump in a pool.
On a hot summer evening, two Best Friends
SG
and
Krishna
decide to jump in a pool.
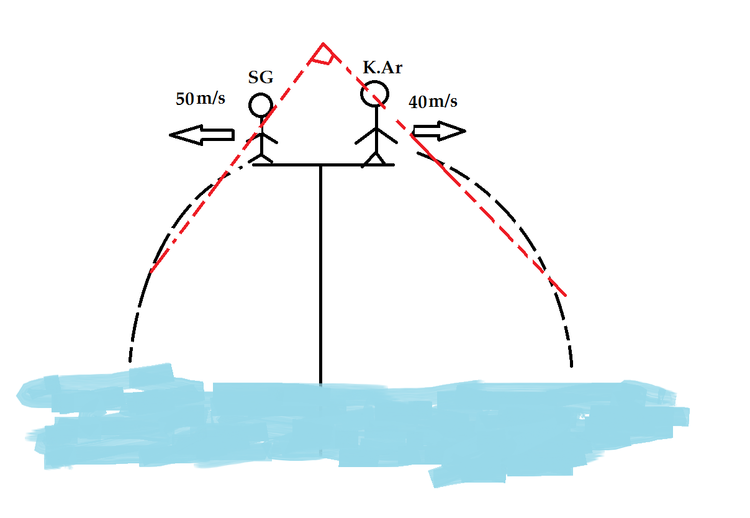
Both of them jumped into the pool at the same time and from the same spot. SG jumped with a horizontal velocity of 5 0 m s − 1 and Krishna jumped with a horizontal velocity 4 0 m s − 1 in the opposite direction.
The time at which their velocities are at 9 0 ∘ with each other is of the form m s . Find m .
(Take g = 1 0 m s − 2 . The image is not to scale.)
The answer is 20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
@Satvik Golechha , @Krishna Ar
Solved the same way....
I solved it as follows with a geometric approach,
If you draw vector diagrams of the velocities of two boys, y-component (let's call it 'v') will be same for both (gravity affects y-component of both of them) and x-component will be 50 and 40 in opposite direction.
Now, If the resultant of 'v' and 50 makes an angle theta with SG's x-velocity,
Then the resultant of 40 and 'v' should make the same angle theta with y-velocity 'v', for the two resultants to be perpendicular.
This gives, tan − 1 5 0 v = tan − 1 v 4 0
which gives v= 2 0 0 0 and ultimately, since v=u+gt, and g=10,u=0, t= 2 0
Vector approach for solving this problem is the best way
We know that v = u + at so , In vector notation let i = +ve direction of x and j= -ve direction of y axis so speed of SG = v1 = 40i +10t speed of krishna = -50i+ 10t as the time when their velocities are mutually perpendicular, their velocities' dot product must be 0 by that we get, 100(t^2)-2000 = 0 It implies that t = sqrt(20) Hence our answer is 20
Let the time taken = t;
After time "t", velocities of
SG = (-50)i + (-gt)j
Krishna = (40)i + (-gt)j
{where
As their velocities are perpendicular at time "t";
dot product of their velocities must be equal to zero:
=> ( (-50)i + (-gt)j ) . ( (40)i + (-gt)j ) = 0
=> g 2 t 2 = 2 0 0 0
=> t 2 = 2 0
I humbly request @shubhendra singh to correct the uploaded answer