What if the variables were not integers?

From $\begin{cases} a + 3 b + 2 ab = 12.965 & \implies b_n = \dfrac {12.965-a_{n-1}}{3+2a_{n-1}} \\ 5 b + 2 c + 9 bc = 111.375 & \implies c_n = \dfrac {111.375-5b_{n-1}}{2+9b_{n-1}} \\ 4 c + 4 a + 10 ac = 73.37 & \implies a_n = \dfrac {73.37-4c_{n-1}}{4+10c_{n-1}} \end{cases}$

Using the simple iteration of assuming $a_0 = 1$ , then compute $b_1$ , $c_1$ and $a_1$ with the above formulas, then $b_2$ , $c_2$ and $a_2$ and so on, with an Excel spreadsheet, the results are:

$\begin{cases} a=1.13 \\ b = 2.25 \\ c = 4.5 \end{cases} \implies 10(a+b+c) = \boxed{78.8}$

Using the multi-variable Newton-Raphson method, we define our vector function as follows:

$f = \begin{bmatrix} a + 3 b + 2 a b - 12.965 \\ 5 b + 2 c + 9 bc - 111.375 \\ 4c + 4a + 10 a c - 73.37 \end{bmatrix}$

Next, we derive the jacobian matrix,

$J = \begin{bmatrix} 1 + 2 b && 3 + 2 a && 0 \\ 0 && 5 + 9 c && 2 + 9 b \\ 4 + 10 c && 0 && 4 + 10 a \end{bmatrix}$

Starting with an initial guess $x_0 = (a_0, b_0, c_0)$ , we apply the Newton-Raphson recursion,

$x_{i+1} = x_i - {J_i}^{-1} f_i$

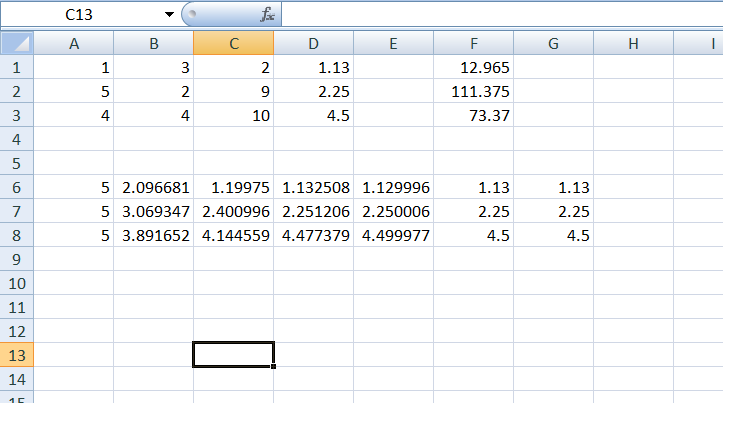
Here's a listing of the successive approximations of the solution as implemented using MS-Excel,

The initial guess is $x_0 = (5, 5, 5)$ .

The trick to solving the system of equations is to apply the concept of Simon's favorite factoring trick (SFFT) .

For simplicity sake, let $D,E,F$ denote the values of $12.965, 111.375, 73.37$ , respectively. We have

$\begin{cases} a + 3b + 2ab = D \\ 5b + 2c + 9bc = E \\ 4c + 4a + 10ac = F \end{cases} \quad \Leftrightarrow \quad \begin{cases} 2a + 6b + 4ab =2D \\ 5b + 2c + 9bc = E \\ 40c + 40a + 100ac = 10F \end{cases} \quad \Leftrightarrow \quad \begin{cases} 2a + 6b + 4ab + 3 =2D + 3 \\ 5b + 2c + 9bc + \dfrac{10}9 = E + \dfrac{10}9 \\ 40c + 40a + 100ac + 16 = 10F+16 \end{cases} \\ \Leftrightarrow \quad \begin{cases} (2a + 3)(2b+1) =2D + 3 \\ \left(3b + \dfrac23\right) \left( 3c + \dfrac53\right)= E + \dfrac{10}9 \\ (10a+4)(10c+4) = 10F+16 \end{cases} \quad \Leftrightarrow \quad \begin{cases} (2a + 3)(2b+1) =2D + 3 \qquad\qquad (\bigstar) \\ (9b+2)(9c+5)= 9E + 10 \qquad\qquad (\bigstar\bigstar) \\ (10a+4)(10c+4) = 10F+16 \qquad (\bigstar\bigstar\bigstar) \end{cases}$

From here, it should be relatively straightforward (but still very tedious) to solve this system of equations to obtain the only positive triplets $(a,b,c) = (1.13,2.25, 4.5)$ .