What Is The Student ID Of Nur Uddin Vai?
Md Nur Uddin is a student of Mathematics Discipline Of Khulna University. Now, you have to find his student ID by solving the following system of linear equations:
− 3 x + 2 y − 6 z 5 x + 7 y − 5 z x + 4 y − 2 z = 6 = 6 = 8 .
If the solution satisfies x + y = z , what is the value of x + y , or equivalently z ?
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
It should be 430z=430
x+y=z
1. Substitute (x+y) for z into two of the equations
-3x+2y- 6z=6
-3x+2y- 6(x+y)=6
-3x+2y-6x-6y=6
-9x-4y=6
x+4y-2z=8
x+4y-2(x+y)=8
x+4y-2x-2y=8
-x+2y=8
2. Next, we use elimination.
-9x-4y=6
-x+2y=8
Multiply the second equation by 2 to get the y terms to cancel.
2(-x-2y)=2(8)
-2x+4y=16
-9x-4y=6
-2x+4y=16
Y terms cancel
-9x=6
-2x=16
-9x-2x=6+16
-11x=22
x = -2
3. Substitute -2 for x to solve for y
-x+2y=8
-(-2)+2y=8
2+2y=8
2y=6
y=3
x+y=z
-2+3=z
1=z
Multiply second equation by 3 and third by 2 you will get
15x + 21y - 15z = 18
2x + 8y - 4z = -16
Subtract second from first. You will get
13x + 13y - 11z = 2
13 (x + y) - 11z = 2
13z - 11z = 2, 2z = 2, z = 1
The real trick here was to manipulate the two equations in such a way that x and y coefficients are equal and that again is no rocket science but pure maths. If we look at the coefficients we see that in first equation y is 2 more than x and in second it is 3 more. We cannot get them equal by adding them so we have to subtract one from other. Now comes the intelligent part. So if we multiply first equation with 3 then y would be 6 more than x. And when we reverse the signs and multiply the second one by 2, x will be 6 more than y. Now if we add together the coefficients will be equal.
⎩ ⎪ ⎨ ⎪ ⎧ − 3 x + 2 y − 6 z = 6 5 x + 7 y − 5 z = 6 x + 4 y − 2 z = 8 Solving: − 1 5 x + 1 0 y − 3 0 z = 3 0 1 5 x + 2 1 y − 1 5 z = 1 8 3 1 y − 4 5 z = 4 8 − 5 x − 2 0 y + 1 0 z = − 4 0 − 1 3 y + 5 z = − 3 4 4 0 3 y − 5 8 5 z = 6 2 4 4 0 3 y + 1 5 5 z = 1 0 5 4 − 4 3 0 z = 4 3 0 z = − 1
− 3 x + 2 y − 6 z = 6 ( 1 )
5 x + 7 y − 5 z = 6 ( 2 )
x + 4 y − 2 z = 8 ( 3 )
Multiply ( 1 ) by 5 and ( 2 ) by 3 , then add the results to eliminate x
5 ( − 3 x + 2 y − 6 z = 6 ) ⟹ − 1 5 x + 1 0 y − 3 0 z = 3 0 ( 4 )
3 ( 5 x + 7 y − 5 z = 6 ) ⟹ 1 5 x + 2 1 y − 1 5 z = 1 8 ( 5 )
Add the results
( 4 ) + ( 5 ) ⟹ 3 1 y − 4 5 z = 4 8 ( 6 )
Now, we must eliminate x in ( 2 ) and ( 3 ) . Multiply ( 3 ) by − 5 then add to ( 2 ) to eliminate x .
− 5 ( x + 4 y − 2 z = 8 ) ⟹ − 5 x − 2 0 y + 1 0 z = − 4 0 ( 7 )
( 2 ) + ( 7 ) ⟹ − 1 3 y + 5 z = − 3 4 ( 8 )
Multiply ( 8 ) by 9 then add to ( 6 ) to eliminate z and solve for y .
9 ( − 1 3 y + 5 z = − 3 4 ) ⟹ − 1 1 7 y + 4 5 z = − 3 0 6 ( 1 0 )
( 6 ) + ( 1 0 ) ⟹ − 8 6 y = − 2 5 8 ⟹ y = 3
Solve for z in ( 8 ) by substituting 3 for y .
− 1 3 ( 3 ) + 5 z = − 3 4 ⟹ − 3 9 + 5 z = − 3 4 ⟹ z = 1
Solve for x in ( 1 ) or ( 2 ) or ( 3 ) . In here, I used ( 3 ) because there is no coefficient of x
x + 4 ( 3 ) − 2 ( 1 ) = 8 ⟹ x = − 2
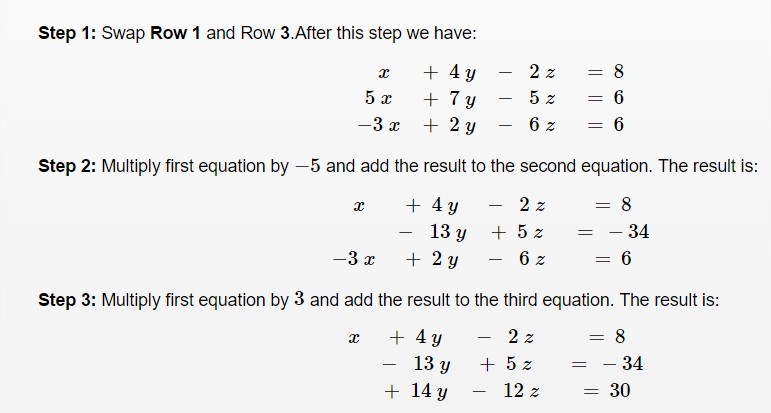

− 3 x + 2 y − 6 z = 6 ( 1 )
5 x + 7 y − 5 z = 6 ( 2 )
x + 4 y − 2 z = 8 ( 3 )
Multiply ( 1 ) by 5 and multiply ( 2 ) by 3 then add the results: ⟹ 3 1 y − 4 5 z = 4 8 ( 4 )
Multiply ( 3 ) by − 5 then add the result to ( 2 ) : ⟹ − 1 3 y + 5 z = − 3 4 ( 5 )
Multiply ( 4 ) by 1 3 and multiply ( 5 ) by 3 1 then add the results: ⟹ − 4 3 0 z = 4 3 0 ⟹ z = 1