What is its Area?

Geometry Level 4

A circle with center point A A and radius 9 c m 9cm touches another circle of radius 5 c m 5cm and center point B B .

Two distinct direct common tangent lines P Q ‾ \overline{PQ} and R S ‾ \overline{RS} are drawn to the circles such that points P P and S S lies on the circle with center A A .

If the area of quadrilateral P Q R S PQRS is △ c m 2 \triangle cm^2 , then find ⌊ △ ⌋ \lfloor \triangle \rfloor .

Note:


The answer is 172.

Zakir Husain by Zakir Husain , 41, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Hongqi Wang
Dec 24, 2020

Let ∠ P A B = θ \angle PAB = \theta

P Q = R S = ( r A + r B ) 2 − ( r A − r B ) 2 = ( 9 + 5 ) 2 − ( 9 − 5 ) 2 = 6 5 sin ⁡ θ = P Q A B = 3 7 5 cos ⁡ θ = 1 − sin ⁡ 2 θ = 2 7 S P Q B A = 1 2 ⋅ ( r A + r B ) ⋅ P Q = 1 2 ⋅ ( 9 + 5 ) ⋅ 6 5 = 42 5 S △ P A S = 1 2 r A 2 sin ⁡ 2 θ = r A 2 sin ⁡ θ cos ⁡ θ = 9 2 ⋅ 3 7 5 ⋅ 2 7 = 486 49 5 S △ Q B R = 1 2 r B 2 sin ⁡ 2 θ = r B 2 sin ⁡ θ cos ⁡ θ = 5 2 ⋅ 3 7 5 ⋅ 2 7 = 150 49 5 S P Q R S = 2 S P Q B A − S △ P A S + S △ Q B R = 2 ⋅ 42 5 − 486 49 5 + 150 49 5 = 540 7 5 ≈ 172.497 ⌊ S P Q R S ⌋ = 172 \begin{aligned} PQ = RS &= \sqrt {(r_A+r_B)^2 - (r_A-r_B)^2} \\ &= \sqrt {(9+5)^2 - (9-5)^2} \\ &= 6\sqrt 5 \\ \sin \theta &= \dfrac {PQ}{AB} = \dfrac 37 \sqrt 5 \\ \cos \theta &= \sqrt {1- \sin^2 \theta} = \dfrac 27 \\ S_{PQBA} &= \dfrac 12 \cdot (r_A+r_B) \cdot PQ \\ &= \dfrac 12 \cdot (9+5) \cdot 6\sqrt 5 \\ &= 42\sqrt 5 \\ S_{△PAS} &= \dfrac 12 r_A^2 \sin {2\theta} = r_A^2 \sin {\theta} \cos {\theta} \\ &= 9^2 \cdot \dfrac 37 \sqrt 5\cdot \dfrac 27 \\ &= \dfrac {486}{49} \sqrt5 \\ S_{△QBR} &= \dfrac 12 r_B^2 \sin {2\theta} = r_B^2 \sin {\theta} \cos {\theta} \\ &= 5^2 \cdot \dfrac 37 \sqrt 5\cdot \dfrac 27 \\ &= \dfrac {150}{49} \sqrt5 \\ S_{PQRS} &= 2S_{PQBA} - S_{△PAS} + S_{△QBR} \\ &= 2 \cdot 42 \sqrt 5 - \dfrac {486}{49} \sqrt5 + \dfrac {150}{49} \sqrt5 \\ &= \dfrac {540}{7} \sqrt5 \\ & \approx 172.497 \\ \lfloor S_{PQRS} \rfloor &= \boxed {172} \end{aligned}

1 Helpful 2 Interesting 2 Brilliant 0 Confused
Hosam Hajjir
Dec 24, 2020

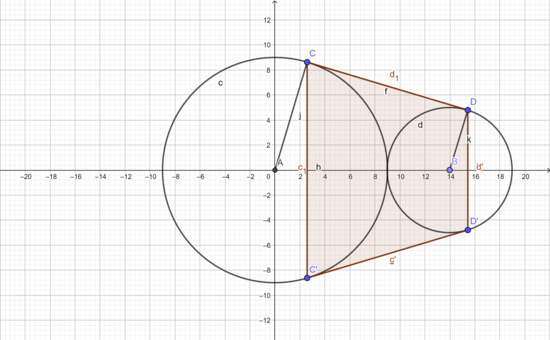
The two circles are depicted in the figure, as well as the quadrilateral C C ′ D ′ D C C' D' D (shaded).

If the slope of C D = − tan ⁡ θ CD = - \tan \theta , then sin ⁡ θ = 9 − 5 9 + 5 = 2 7 \sin \theta = \dfrac{9 - 5}{9+5} = \dfrac{2}{7} and cos ⁡ θ = 45 7 \cos \theta = \dfrac{\sqrt{45}}{7}

The coordinates of point C = ( C x , C y ) = ( 9 sin ⁡ θ , 9 cos ⁡ θ ) C = (C_x, C_y) = (9 \sin \theta, 9 \cos \theta ) , and the coordinates of point D = ( D x , D y ) = ( 14 + 5 sin ⁡ θ , 5 cos ⁡ θ ) D = (D_x , D_y) = ( 14 + 5 \sin \theta, 5 \cos \theta)

Hence, the area of the trapezoid is

[ C C ′ D ′ D ] = ( 14 cos ⁡ θ ) ( 14 − 4 sin ⁡ θ ) = 2 45 ( 14 − 8 7 ) ≈ 172.49667 [C C' D' D ] = (14 \cos \theta) (14 - 4 \sin \theta) = 2 \sqrt{45} (14 - \dfrac{8}{7} ) \approx 172.49667

Hence the answer is 172 \boxed{172}

2 Helpful 2 Interesting 2 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...