What is now this limit doing here?
Find x → 2 π lim ( sin x − cos x ) tan x The limit above has a closed form. Find the value of this closed form.
For example, submit your answer to 8 decimal places.
The answer is 0.36787944.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
wow!, I loved this wonderful "no-standard" approach (solution). Thank you, sir (+1) ↑ .
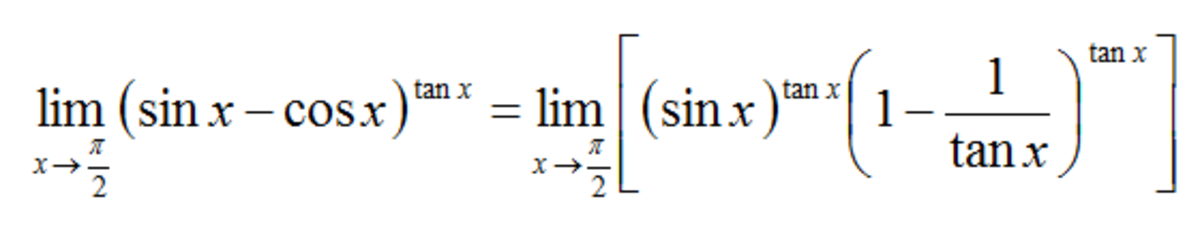
Log in to reply
hm, I understand you, It still need to be proved x → 2 π lim ( sin x ) tan x = 1 ..... Good reply.....
By inserting the limit, we can clearly see that the expression takes the form 1 ∞ , which can be easily solved by using the exponential conversion. So, the following limit can be written as:
e lim x → 2 π ( sin x − cos x − 1 ) tan x
Which can be further simplified into
e lim x → 2 π cot x ( sin x − cos x − 1 )
Now, as we can clearly see that the limit in the exponent tends to a 0 0 form, so we'll use the L'Hôpital's Rule to simplify it further.
Differentiating the numerator and denominator in the power, with respect to x , we get:
e lim x → 2 π − csc 2 x cos x + sin x
Now, inserting the limit into the formed expression:
e − 1 0 + 1 = e − 1 = 0 . 3 6 7 8 7 9 4 4
Cheers! :)
Thank you for your solution. (+1) ↑
x → 2 π lim ( sin x − cos x ) tan x = x → 2 π lim sin x ( 1 − tan x 1 ) tan x Let n = tan x = x → 2 π lim sin x ⋅ n → ∞ lim ( 1 − n 1 ) n = 1 ⋅ e 1 ≈ 0 . 3 6 7 8 7 9 4 4