What is the 7th term?

nth term is 7 and initial number is 2 and common difference in sequence is 5,so we know the formula tn=a1+d(n-1) Put the value in this, t7=2+5(7-1)=32 t7=32

Common difference is $5$ .

$2+6(5)=\boxed{32}$

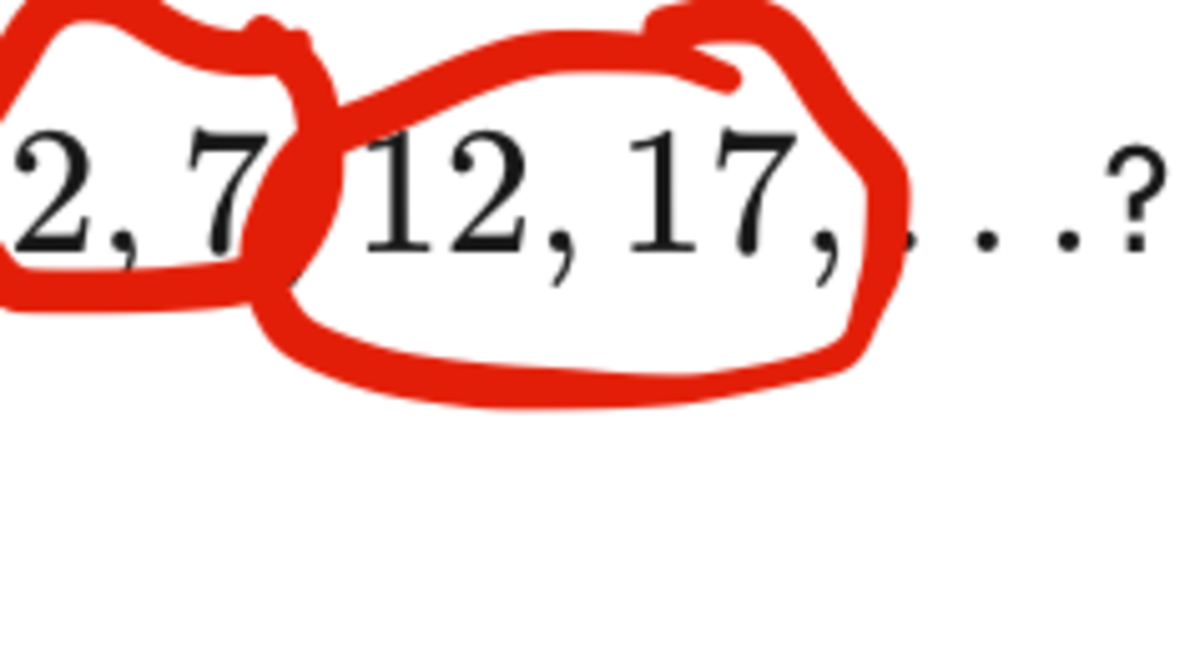
Look at it in pairs. _2 is always odd so 7th is _2. 1&2, 3&4 share the tens digit, so 7&8 also share the tens digit. The tens digit is the 2nd number in a pair divide by 2 and minus 1. Therefore, the answer is 7.

We have that: $a_{n} = a_{1} + d(n - 1)$

---

• To get $a_{1}$ , we just choose the first number of our series, that in $2, 7, 12, 17,...$ , is $2$ .

  So, we get that $a_{1} = 2$

---

• Then, to get $d$ , we could calculate the difference of two consecutive numbers using the formula $(a_{n+1} - a_{n})$ .

  For example: $(7 - 2 = 5)$ , and if we want to corroborate, we could just repeat it with some different consecutive numbers, like $(12 - 7 = 5)$ or $(17 - 12 = 5)$ .

  So, we get that $d = 5$

---

• Finally, to get $n$ , we just check the text, and it says that we need to know the seventh term.

  So, we get that $n = 7$

---

Now, we can substitute on our main formula:

$\\a_{n} = a_{1} + d(n - 1)\\ a_{n} = 2 + 5(7 - 1)\\ a_{n} = 2 + 30\\ \boxed{a_{n} = 32}$

The nth term of an arithmetic progression is:-

$t_{n}=a+(n-1)d$ where a is the first term, and d is the common difference.

Putting n=7, we get it as 32.