What is the area of the green triangle?
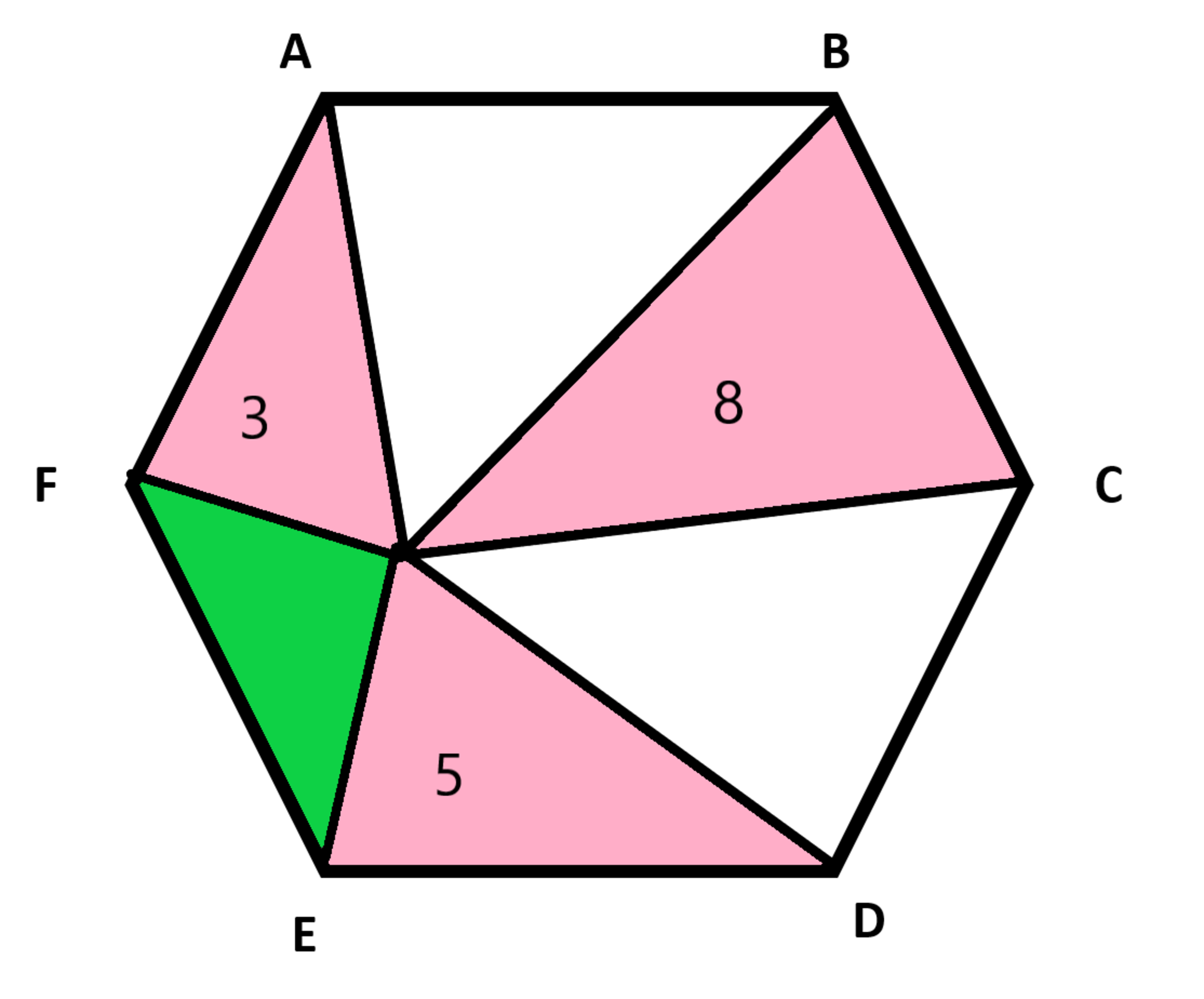
There is a point inside a regular hexagon. It forms six triangles with the vertices.
The area of the green triangle is of the form b a , where a and b are co-prime.
Input a + b as your answer.
The answer is 11.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Can you please elaborate on how did you find that the pink area is exactly half the area of the hexagon from this two triangles.
Log in to reply
Say the perpendicular distances from the sides of the hexagons to the point P are h A B , h B C , etc (these are the heights of the triangles).
Viviani's theorem (linked above) implies that h A B + h C D + h E F = h B C + h D E + h F A .
Since the bases of the triangles are all the same, say b (the side of the hexagon), this means the pink area is the same as the non-pink area; so must be half the area of the hexagon.
I've never heard of that theorem, but while solving, I encountered this and wished if it were true
Log in to reply
The way I solved it originally was actually coordinate geometry; it was only after that I noticed there might be a shortcut. The property that the pink triangles are exactly half the hexagon reminds me a bit of the pizza theorem (though it's not quite the same).
The crucial point is making an equilateral triangle out of the hexagon. This really simplifies the calculation.
Let the side length of the regular hexagon be a and its center be the origin O ( 0 , 0 ) of the x y -plane. Then A ( − 2 a , 2 3 a ) , B ( 2 a , 2 3 a ) , C ( a , 0 ) , D ( 2 a , − 2 3 a ) , E ( − 2 a , − 2 3 a ) , and F ( − a , 0 ) . Let the point inside the hexagon be P ( x , y ) . We can find area using the coordinates. For △ P B C :
2 1 ( 2 a − x ) ( 2 3 a + y ) + 2 1 ( a − 2 a ) ( 0 − 2 3 a ) + 2 1 ( x − a ) ( y − 0 ) 4 3 a 2 − 2 3 a x + 2 a y − x y + 4 3 a 2 + x y − a y ⟹ 2 3 a 2 − 2 3 a x − 2 a y = 8 = 1 6 = 1 6 . . . ( 1 )
For △ P D E (just half base times height):
2 a ( y + 2 3 a ) ⟹ 2 3 a 2 + a y = 5 = 1 0 . . . ( 2 )
For △ P F A :
2 1 ( − a − x ) ( 0 + y ) + 2 1 ( − 2 a + a ) ( 2 3 a + 0 ) + 2 1 ( x + 2 a ) ( y + 2 3 a ) − a y − x y + 4 3 a 2 + x y + 2 a y + 2 3 a x + 4 3 a 2 ⟹ 2 3 a 2 + 2 3 a x − 2 a y = 3 = 6 = 6 . . . ( 3 )
From 2 ( 1 ) + ( 3 ) : ⟹ 2 3 a 2 − 2 a y = 1 1 . . . ( 4 ) . From ( 2 ) − ( 4 ) : ⟹ 2 3 a y = − 1 ⟹ 2 a y = − 3 1 . . . ( 5 )
For △ P E F (let its area be A ):
A 2 A ⟹ A = 2 1 ( − 2 a − x ) ( − 2 3 a + y ) + 2 1 ( − a + 2 a ) ( 0 − 2 3 a ) + 2 1 ( x + a ) ( y + 0 ) = 4 3 a 2 + 2 3 a x − 2 a y − x y + 4 3 a 2 + x y + a y = 2 3 a 2 + 2 3 a x + 2 a y = 2 3 a 2 + 2 3 a x − 2 a y + 2 × 2 a y ⟹ ( 3 ) + 2 × ( 5 ) = 6 − 3 2 = 3 1 6 = 3 8
Therefore a + b = 8 + 3 = 1 1 .
Let the interior point be P .
Extend the sides B C , D E , F A so that they meet and form an equilateral triangle. By Viviani's theorem , the sum of the perpendicular distances from P to each of these sides is the same no matter where P is inside the hexagon.
The same is true if we extend the sides A B , C D , E F , and because the triangles have the same size, this constant is the same.
So the pink area is exactly half the area of the hexagon; the area of the hexagon is 3 2 .
Now consider pairs of triangles whose bases are parallel (for example, P E F and P B C ). The sum of their heights is always the same (the distance between two parallel sides of the hexagon). So the sum of their areas is the same for each pair. Since there are three such pairs, and they fill the hexagon, each pair has a total area of 3 3 2 .
So the green triangle has area 3 3 2 − 8 = 3 8 .