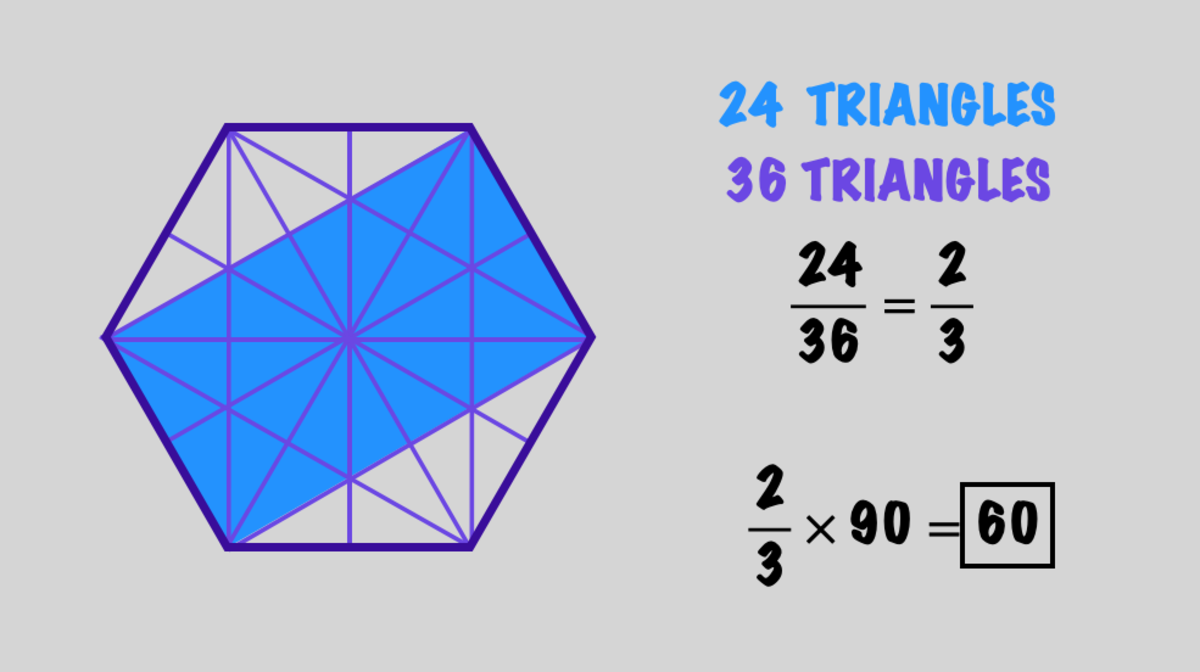
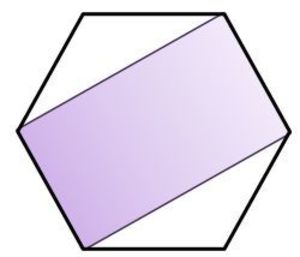
What is the Area of the Purple region??
If the area of the regular hexagon is 9 0 , what is the area of the purple region?
The answer is 60.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
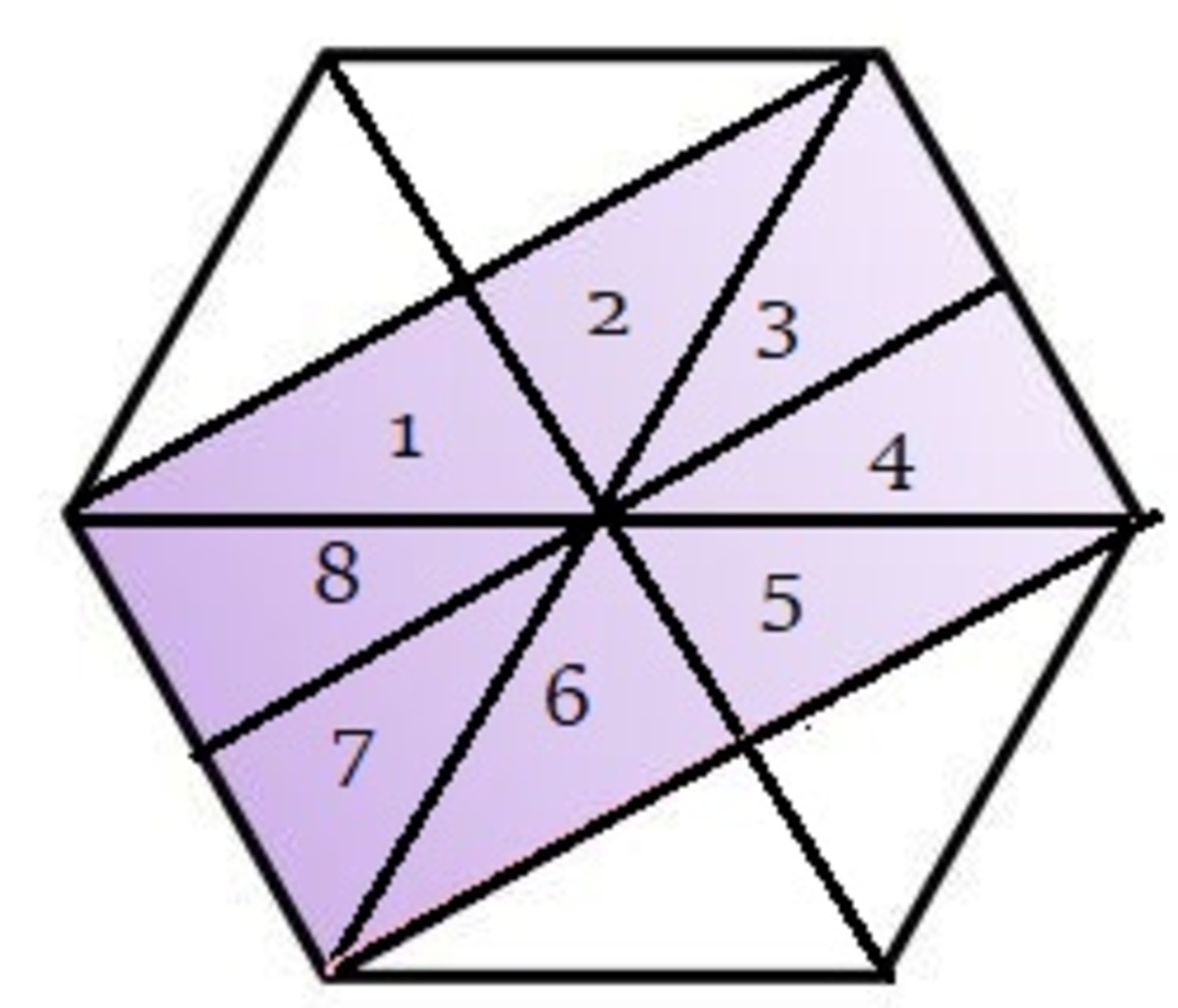 Note that the ratio of the purple region is :
1
2
8
⟹
Area of the purple region is :
1
2
8
(
9
0
)
=
3
2
(
9
0
)
=
6
0
Note that the ratio of the purple region is :
1
2
8
⟹
Area of the purple region is :
1
2
8
(
9
0
)
=
3
2
(
9
0
)
=
6
0
Log in to reply
Thank you for sharing your solution.
I just saw it.
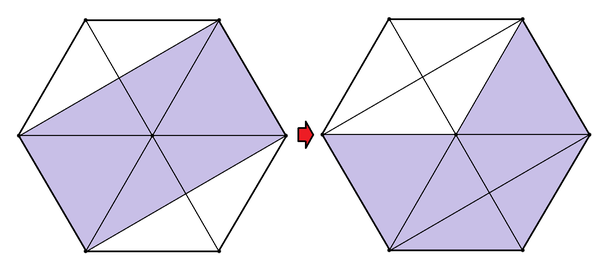
We note that 6 equilateral triangles make up the hexagon of area 9 0 and the area of purple region is equal to 4 equilateral triangles or 6 4 × 9 0 = 6 0 .
Thank you Sir for sharing your solution.
Nice transformation!!
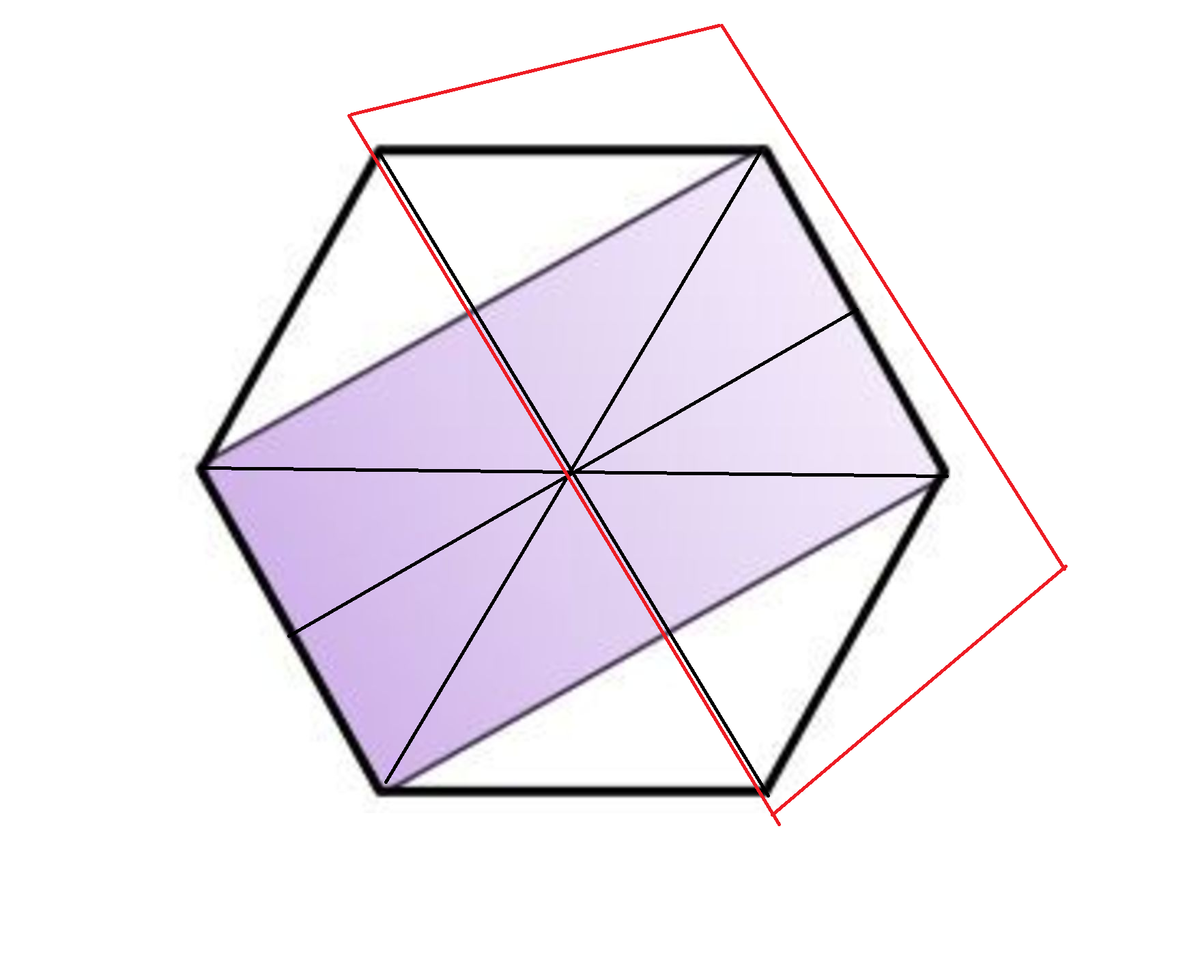
Cut the figure into 1 2 regions using diagonals.
Focus on half of the figure. 4 regions are purple, 2 are not.
Hence, ratio of purple to figure = 4 + 2 4 = 3 2 .
Since whole figure's area = 9 0 ,
Purple area = 3 2 × 9 0 = 6 0
Thank you for sharing your solution.