What is the area of the shaded region?
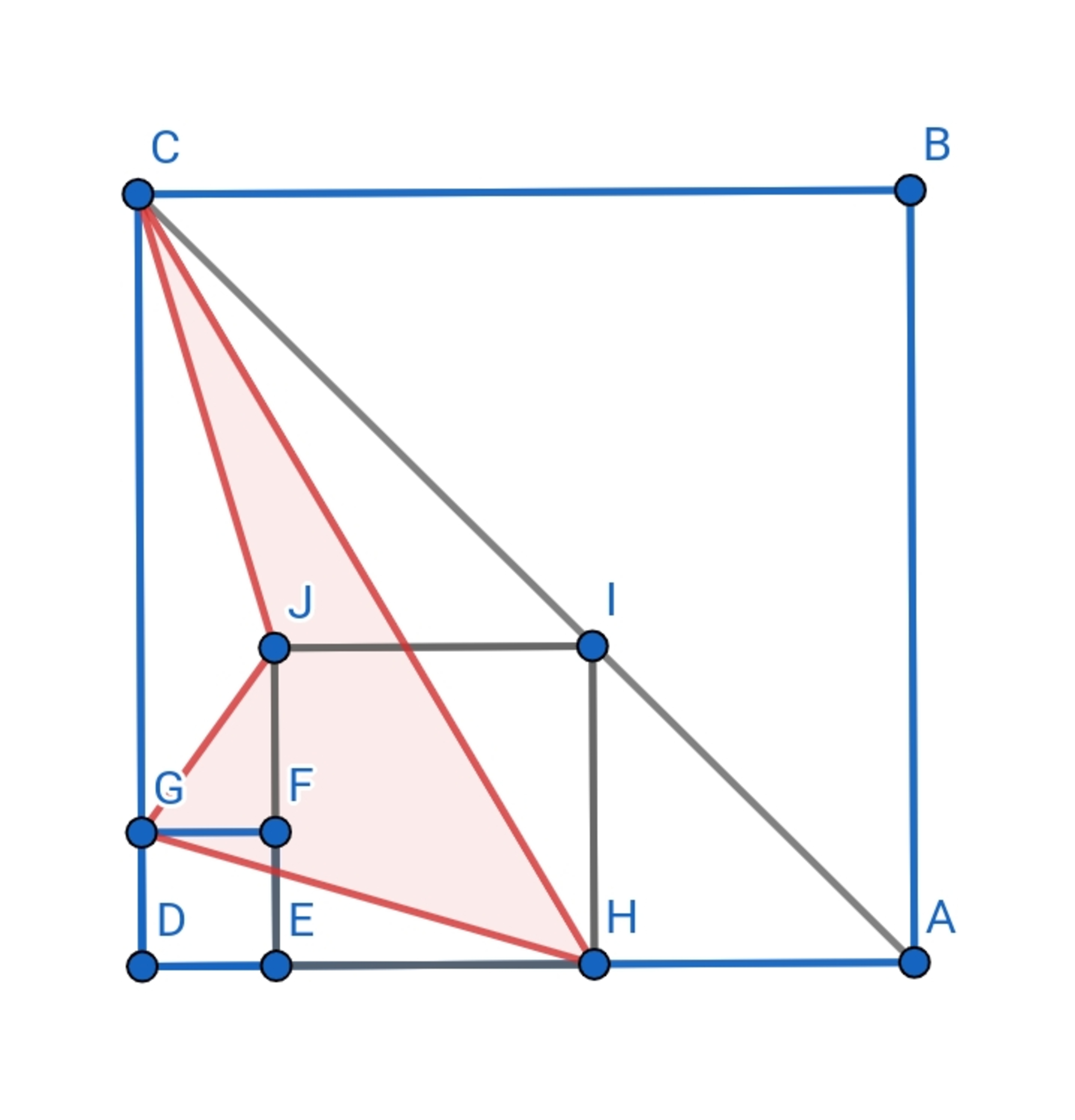
It is known that A B C D , D E F G , E H I J are squares and H J = 4 2 . I is on A C , what is the area of H G J C (region in red)?
The answer is 16.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
 Since
C
A
∥
J
H
∥
G
E
, the transformation we see in the animation preserves the areas of moving triangles with base
J
H
, thus, the area of the red quadrilateral
H
G
J
C
equals the area of the square
J
I
H
E
. But,
[
J
I
H
E
]
=
2
1
J
H
2
.
Hence,
[
H
G
J
C
]
=
2
1
(
4
2
)
2
=
1
6
Since
C
A
∥
J
H
∥
G
E
, the transformation we see in the animation preserves the areas of moving triangles with base
J
H
, thus, the area of the red quadrilateral
H
G
J
C
equals the area of the square
J
I
H
E
. But,
[
J
I
H
E
]
=
2
1
J
H
2
.
Hence,
[
H
G
J
C
]
=
2
1
(
4
2
)
2
=
1
6
Log in to reply
It's irritating that the board doesn't allow me a one-word response.
Squaring a polygon is a hobby of ancient Greek mathematicians. In his Elements, Euclid has solved it before me :)
Nice solution, Thanos!
Place point D at the origin of the x y − plane. Let squares A B C D , D E F G , E H I J each have side lengths equal to p , q , 4 respectively. The red area is bounded by vertices:
C ( 0 , p ) ; G ( 0 , q ) ; H ( q + 4 , 0 ) ; J ( q , 4 )
If point I ( q + 4 , 4 ) lies on diagonal A C , which can be represented as the line y = − x + q , then we have:
4 = − ( p + 4 ) + q ⇒ q = p + 8 .
The red area, C G H J , can be computed as the sum of triangular areas △ G H J and △ C H J :
A C G H J = 2 1 ⋅ ∣ ∣ ∣ ∣ ∣ ∣ ∣ 1 1 1 0 p p + 4 p 4 0 ∣ ∣ ∣ ∣ ∣ ∣ ∣ + 2 1 ⋅ ∣ ∣ ∣ ∣ ∣ ∣ ∣ 1 1 1 0 p p + 4 p + 8 4 0 ∣ ∣ ∣ ∣ ∣ ∣ ∣ = ∣ 2 4 p − 4 p − 1 6 ∣ + ∣ 2 4 p − 4 p − 1 6 + 3 2 ∣ = ∣ − 8 ∣ + ∣ 8 ∣ = 1 6 .
Inelegant (but straightforward) solution:
Goal will be to start with the area of triangle
A
C
D
and subtract areas of triangles
A
H
C
,
G
D
H
, and
C
J
G
.
We are given that the distance
H
J
=
4
2
. Thus the side length of this square is
4
. And since I is on the main diagonal of square
A
B
C
D
,
A
H
=
H
I
=
4
.
We are not given the side length of the small square D E F G , but that will not matter: let x = D E . Then A D = 8 + x and the area of the square A B C D is ( 8 + x ) 2 = 6 4 + 1 6 x + x 2 . And the area of the triangle A C D is half of this quantity, i.e. 3 2 + 8 x + ( 1 / 2 ) x 2 .
The area of triangle A C H is ( 1 / 2 ) ( 8 + x ) 4 = 2 ( 8 + x ) 1 6 + 2 x .
The area of triangle H D G is ( 1 / 2 ) x ( 4 + x ) = 2 x + ( 1 / 2 ) x 2 .
The area of triangle C J G is ( 1 / 2 ) ( 8 ) x = 4 x .
Thus the area of the red shape is ( 3 2 + 8 x + ( 1 / 2 ) x 2 ) − ( 1 6 + 2 x ) − ( 2 x + ( 1 / 2 ) x 2 ) − ( 4 x ) = 1 6 . The terms involving x have disappeared.
If the length of the side, H J = 4 2 , then □ E H I J → I J = H I → I J 2 + H I 2 = ( 4 2 ) 2 → 2 H I = 8 → I J = H I = 4 \cm . Since □ C H G J = □ E H I J , so the area of □ C H G J is 1 6 \cm 2 .