What is the area of the green region?
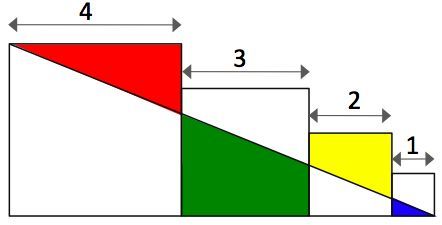 What is the area of the green region? All shapes are squares with the measure side given.
What is the area of the green region? All shapes are squares with the measure side given.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Thank you for sharing your solution.
We note that there are four similar triangles. Let the areas from the smallest triangle (blue) to the largest one be A 1 , A 2 , A 3 and A 4 respectively. Then A 4 = 2 1 × ( 1 + 2 + 3 + 4 ) × 4 = 2 0 . For similar shape figures, the area A is directly proportional to the square of a side length a . That is A ∝ a 2 . Then A 4 A 3 = ( 1 + 2 + 3 + 4 ) 2 ( 1 + 2 + 3 ) 2 = 0 . 3 6 ⟹ A 3 = 0 . 3 6 A 4 = 7 . 2 . Similarly, A 2 = 1 0 2 3 2 A 4 = 0 . 9 × 2 0 = 1 . 8 . The area of the green region A green = A 3 − A 2 = 7 . 2 − 1 . 8 = 5 . 4 .
First we need to take the ratio of proportionality:
1
+
2
+
3
+
4
4
=
0
.
4
.
Then we can calculate the sides of the trapezoid of the green figure as indicated in the given picture.
Thus, the area of the green region is: 2 ( 2 . 4 + 1 . 2 ) × 3 = 5 . 4
Let f be the formula for the line that passes trough (0,4) and (10,0), then f(x) = - 0.4x + 4. So the green area = 0.5(f(4)+f(7))*3 = 5.4.