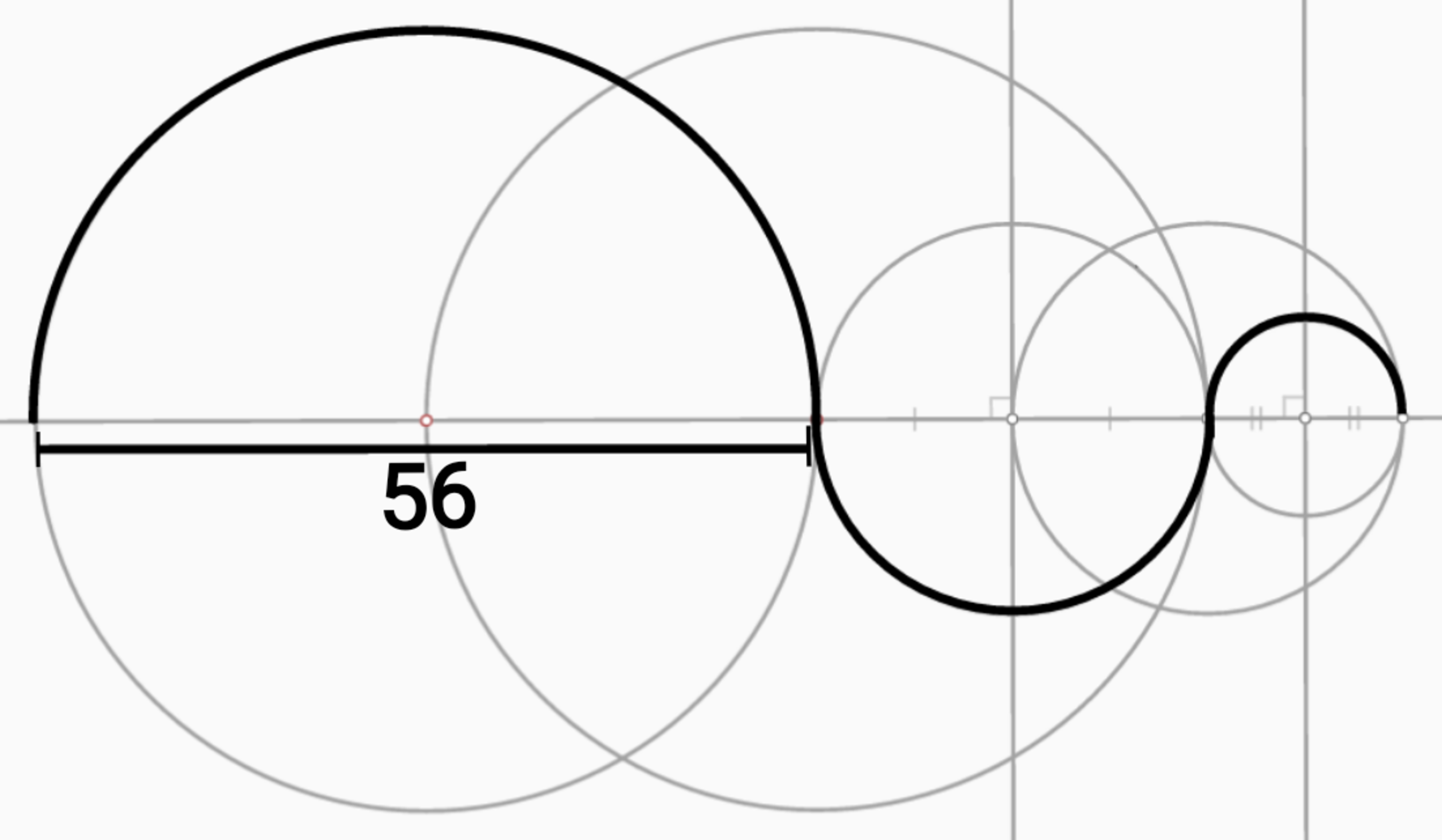
What is the length? (Circles I)

• The radii get halved after each successive circle. Given that diameter of largest circle is $56$ , its radius will be half of that which is $28$ . The next two smaller radii will be $14$ , $7$ respectively.
• The perimeter of half circle is $\frac{2 \pi r}{2} = \pi r$
• The total length of black line will be:

$\begin{aligned} &= \pi(28) + \pi (14) + \pi(7) \\ &= \pi (28 + 14 + 7) \\ &= \dfrac{22}{7}(49) \\ &= \dfrac{22}{\cancel{7}}(\cancel{7} \times 7) \\ &= \boxed{154} \end{aligned}$

Formula to find out the circumference of a semi-circle (excluding the radius)

$\boxed{πr}$

Length of first semi-circle arc

$\frac{22}{7} × 28$

$= \boxed{88}$

Area of second middle semi-circle arc

$\frac{22}{7} × 14$

$= \boxed{44}$

Area of small semi-circle arc

$\frac{22}{7} × 7$

$= \boxed{22}$

Summing them up gives:

$88 + 44 + 22 = \boxed{154}$