What is the length of GF?
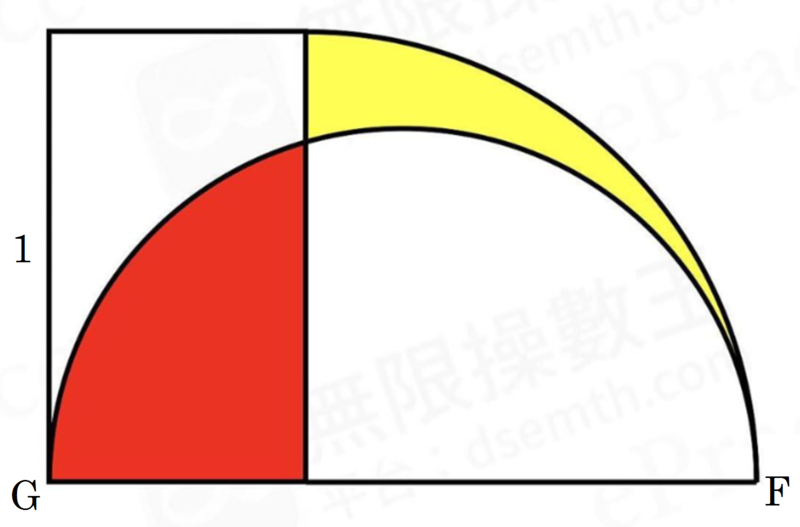
In the figure above there are a rectangle with height 1 , a quadrant of radius 1 , and a semicircle. The red region and the yellow region have the same area. Find G F 2 .
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let the breadth of the rectangle be b and the area of the red region be A . Then A = 4 π − ( 8 π ( b + 1 ) 2 − A ) ⟹ b = 2 − 1 ⟹ ∣ G F ∣ = 2 ⟹ ∣ G F ∣ 2 = 2 .
Let the radius of the semicircle be r and the area of the region be A red . Then the area of the white part of the semicircle is A white = 2 π r 2 − A red , and the area of the yellow region A yellow = 4 π − A white = 4 π − 2 π r 2 + A red . Now we have:
A yellow 4 π − 2 π r 2 + A red 4 π − 2 π r 2 2 π r 2 ⟹ r G F 2 = A red = A red = 0 = 4 π = 2 1 = ( 2 r ) 2 = 2