What is the length of the chord ?
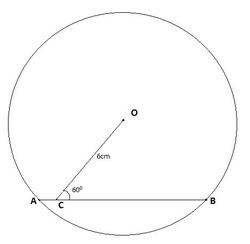 There is a chord AB in a circle with center O. As shown in the figure, a line segment OC makes an angle of 60 degrees with the chord. If OC=6cm and BC=8cm, then find the length of the chord.
There is a chord AB in a circle with center O. As shown in the figure, a line segment OC makes an angle of 60 degrees with the chord. If OC=6cm and BC=8cm, then find the length of the chord.
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
24 solutions
8-6=2 and finally 8+2=10
draw another line from O to the chord at 60.now length of each side of the equilateral triangle thus formed is 6.The length left is 2.Hence chord length is 6+2+2=10
Wow, and here I go using Law of Cosines to find the radius when I clearly could have just did it your way. Nice and simple solution.
cos 60=1/2=x/6... hence x=3... 8-3=5... and finally ac=5-3=2... so AB=AC+BC= 2+8=10....
simple 8-6=2 becz equilateral triangle and 8+2=10
Good question
10
length of the Perpendicular will be 3 root(3) = 6 sin60 and the corresponding base will be 3 = 6*cos60 so half of the chord value 5 only [Perpendicular to chord divide it equally] ] so value is 10
10
BC-OC=AC AC+BC= AB AO=OB 8cm-6cm=2 and finally 8 +2= 10
there is a better approach, draw a line D = 6 0 ° from o such that it touches B C and,now △ C O D is equatorial due to its 6 0 , 6 0 , 6 0 angles. now, C D = 6 c m and D B = 2 c m we can say A C = D B = 2 c m ∴ 6 + 2 + 2 = 1 0
another simpler way, is to construct a line that is 60 degree from o and lies on bc, name it op so angle opc is also 60 degree that is equilateral triangle so pc = 6 cm. From that 8-6 = 2 so 8+2 = 10
simple. no need to use calculator. OC is 6cm, BC is 8cm and angle OCB is 60degrees, if you add another point within segment AB, lets say point D that should give an angle ODC or ODA = 60degrees. You can form a equilateral triangle. All sides of equilateral triangle is equal. So if OC is 6cm, OD and DC is also 6cm. We know that BC is 8cm and DC is 6cm, subtract the 2 segments to get the segment BD, and that would be 2cm. SO, AC is 2cm too. Add the 3 segments AC, CD and BD = 10cm. :) make sense?
very nice
i found it same too
very nice method
Another way. Draw angle ODC=60 and C-D-B. Now triangle OCD is equilateral. So CD=6 and so BD=BC-CD=2.. Same way AD will also be 8 and AC will be 2. So AB=AC+CD+DB=2+6+2=10. No trigonometry required :-)
yeah i thought in the same way no need of trignometry
10 cm (construction drop perpendicular from the center we will get aright angled triangle with 30 and 60 degrees . and the opposite side to the angle 30 equals half the hypotenuse =3 cm so half the chord =8-3 =5 so the chord = 10
It is very easy. Just compute 6 cos 60 = 3 cm which is the length of the projection if the radius on AB. Now AB will half of AB WILL BE 5 cm and AB will be 10 cm.
10
OC=6,Now lets draw a perpendicular OE on the chord ,so the COE is a right triangle,that makes its base CE=6 * cos 60=6 * *1/2=3,now EC=BC-CE=8-3=5,so 1/2 * chord=5 so chord=10
The sum is wrong as, let perpendicular on cord be OP. In triangle OPC. angle OPC is 60deg... hence OP is 3root(3)... in tranangle OAP, angle OAP is 45 .. hence. AP is 3root(3).. hence chord length is 6root(3).. i.e = 10.92
draw an imaginary line OD intersecting AB in such a way that OD=OC=6cm and points C & D do not coincide, thus making an isosceles triangle OCD where OC=OD & angle(OCD)=angle(ODC). Since the two angles are 60 degrees each, then the third angle will be (180-60-60=60). Hence the triangle becomes equilateral triangle. Hence the third side CD=6cm. Now, according to the question, BC=8cm, BD=BC-CD=8-6=2cm. Hence the length of the chord becomes 6+2+2=10cm
if we draw a line OD such a way that angle(ODA)=60 degree this will be a equilateral triangle and OD=6 and CD=6...so DB=8-6=2....so AC=2..since AC=BD..total AB=AC+BC=2+8=10...
Let's suppose a line segment OD is drawn , as if OD perpendicular AB. Here, sin60= OD/OC = 5.2 and cos60= DC/OC =3. We know that BC=8cm.Means, CD+DB=BC= 8cm. We know that, a perpendicular from the center to a chord divides the chord in half. So, DB = 8-3=5cm. so, AB=2DB= 10. Answer= 10 cm
We draw aperpendicular from o to chord AB as OD.Now with OCD trianle ,side OC is 6 Cm and angle C is 60 degree so CD is 3 cm and therefor BD is 5 cm..OD is 3underroot 3.(hay h) Now from trianle ODB we canculate OB( radius as underroot 52, from h=3underroor3 and DB as 25) Length of chord = 2 underroot rs quare - h square +2 X5 + 10 Ans.
K.K.GARGIndia
10 thats a simple use of trigonometry
Draw a segment OD to any point of BC that will make a 60 degree angle namely, angle D then a triangle BOD is formed , so, angle O is also 60 degrees, since all angles of the triangle BOD are equal so the sides are also equal, where BO=BD=OD=6. Since the length of BD= 8 - DC, then BD=6, so, DC=2, where DC=AB so, AC=AB+DB+DC=2+6+2=10
drop a perpendicluar ol to chord ab .. in triangle olc angle olc =90 so by trigonometry ab lc=occos60 i.e 6 1/2=3 now bc=bl+lc 8=bl+3 bl= 5 ol is perpendicluar to chord ab it also divides it into two equal parts so ab =2bl =2 5=10
Drop a perpendicular on AB from centre O. Let this perpendicular meet at X on AB. Then, CX = 6 cos60 = 3. So, BX = 8-3 =5. As perpendicular on chord from centre bisects it into two equal parts, AX=BX. Therefor, AB=2BX= 2x5=10.
CH=cos OCB. OC= cos60.6=1/2.6=3 BH = BC - CH = 8- 3=5 as BH=1/2 . AB -> AB=10.
if you consider a point on the chord D forming a equilateral triangle....then yoy can find the length DB and from there you can infer the length i.e AC+CD+DB+10
draw a perpendicular from O to chord AB.mark as D.in triangle OCD find OD.now in tiangle OCB apply cosine law ,OB^2=OC^2+BC^2 - 2 OC BCCos(60).In triangle ODB,find BD, using pythagoras theorem, In a circle perpendicular from centre on chord divides the chord into two equal halves.therefore,AB=2*BD=10
consider a perpendicular bisector from center to the chord now if we take cos60 then we get lenght of cto the pt the pt on the bisector line on the chord now sub that lenght from given value lt of chrd we get 5 make it double we get the lt of the chord
BC=8cm and angle ADO=60 degree so the triangle is equilateral and all side are 6 cm their fore 8-6=2 therefore its 10 cm.
Draw line OD perpendicular to the chord AB. OD = Sin60 * 6. CD = cos60 * 6 = 3 cm. Now, DB = BC - CD = 5 cm. So, AB = 2* DB = 10 cm
join O with B and calculate OB by using cosine law i:e a2=b2+c2-2abcosA tha t will be radius.than apply same formula on triangle OCA and calculate length AC=2 than calculate AC+CB=10
why don't we try to place another line that has an angle 60 degree, so all the sides of the triangle will be 60 degree which means all will have the same length. Then try minus 8 with 2 so the length on the other will be the same. you get me once you try.Enjoy
Good solution
Consider a line segment OD which is a perpendicular bisector of AB. As cos60 = DC/OC, we get DC = 3. Now BC = DC + BD from which we get BD = 5. Length of the chord AB is 2 x BD = 10.