What is the length of the radius of the circle
ABCD is a cyclic quadrilateral.
AB = 9 cm BC = 7 cm CD = 6 cm AD = 2 cm
Find the length of the radius of the circumcircle of this quadrilateral in centimetres.
Type in the square of the length of the radius into the answer box as a decimal fraction.
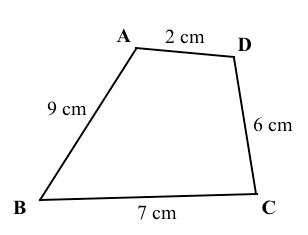
If there is not enough information given in the diagram to find the length of the radius, type in -1 as the answer.
The answer is 21.25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Consider BD. Using the cosine rule for △ A B D and △ B C D , we obtain:
B D 2 = A B 2 + A D 2 − 2 . A B . A D cos ( ∠ B A D )
B D 2 = B C 2 + C D 2 − 2 . B C . C D cos ( ∠ B C D )
Equating these, we obtain:
A B 2 + A D 2 − 2 . A B . A D cos ( ∠ B A D ) = B C 2 + C D 2 − 2 . B C . C D cos ( ∠ B C D )
However, A B 2 + A D 2 = B C 2 + C D 2 = 8 5 .
So:
2 . A B . A D cos ( ∠ B A D ) = 2 . B C . C D cos ( ∠ B C D )
A B . A D cos ( ∠ B A D ) = B C . C D cos ( ∠ B C D )
Since ABCD is a cyclic quadrilateral, ∠ B C D = 1 8 0 ∘ − ∠ B A D .
1 8 cos ( ∠ B A D ) = 4 2 cos ( 1 8 0 ∘ − ∠ B A D )
In general, cos ( θ ) = cos ( 1 8 0 ∘ − θ ) . So:
1 8 cos ( ∠ B A D ) = 4 2 cos ( ∠ B A D )
0 = ( 4 2 − 1 8 ) cos ( ∠ B A D )
0 = cos ( ∠ B A D )
∠ B A D = 9 0 ∘ (as ∠ B A D lies between 0 ∘ and 1 8 0 ∘ )
Therefore, [BD] is a diameter of the circle.
B D = 8 5
This means that the radius, r = 2 8 5
Squaring the radius gives: 4 8 5 = 21.25