What is the limit volume of this figure as n goes to infinity?

Note: I am asking for a numeric answer. If you can determine the answer without actually figuring out the limit, then that is OK.

The absolute values of $x$ , $y$ and $z$ are $\leq 1$ . $n$ is a positive even integer, i.e., $n \bmod 2=0$ . The values are all $\mathbb{R}$ .

What is the limit as $n\to +\infty$ from below of the volume of the figure such that $(x^n+y^n+z^n)\leq 1$ is true and the absolute values of $x$ , $y$ and $z$ are $\leq 1$ .

For your assistance, here are two pictures from the beginning of the sequence.

For n=2,

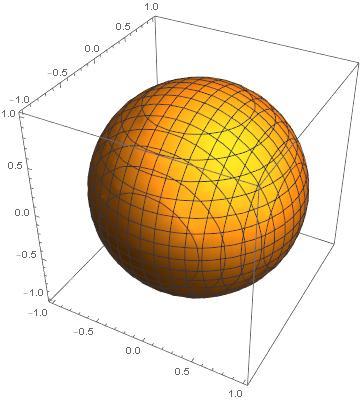
For n=4,

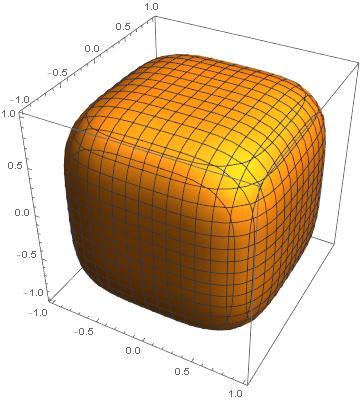
This is not a requirement to solve this problem. If you like, then determining this limit will give you a major clue:

$\text{Assuming}\left[\left| x\right| \leq 1,\underset{n\to \infty }{\text{lim}}\ \underset{x\to 1}{\text{lim}} \ x^n\right]$