This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
 Essentially, if ABCD was stacked by a figure of the same proportions, it would create a square in the middle. This means that the square's diagonal will create a 45-45-90 triangle. This means that the blue angle must be 45 degrees.
Essentially, if ABCD was stacked by a figure of the same proportions, it would create a square in the middle. This means that the square's diagonal will create a 45-45-90 triangle. This means that the blue angle must be 45 degrees.
We can see that triangle ABE and triangle ECD are congruent since they are both right triangles and have congruent legs..Since angle BEA is congruent to angle CDE, congruent triangles, BEA+CDE=90degrees.So angle AED is180-90 which is 90 degrees. Since triangle ABE and triangle ECD are congruent, the hypothenuses are congruent which makes triangle AED a isosceles right triangle which makes angel ADE 45 degrees.
Simply amazing

cos a = 5 2 5 2 = 2 1 2 So, a = 4 5
We Have D C ˉ = B E ˉ and A B ˉ = E C ˉ , so both triangles are of equal size and then A E ˉ = D E ˉ
Since the triangle AED is isosceles and has a right angle (90 degrees), we can say that any of the remaining angles has 45 degrees.
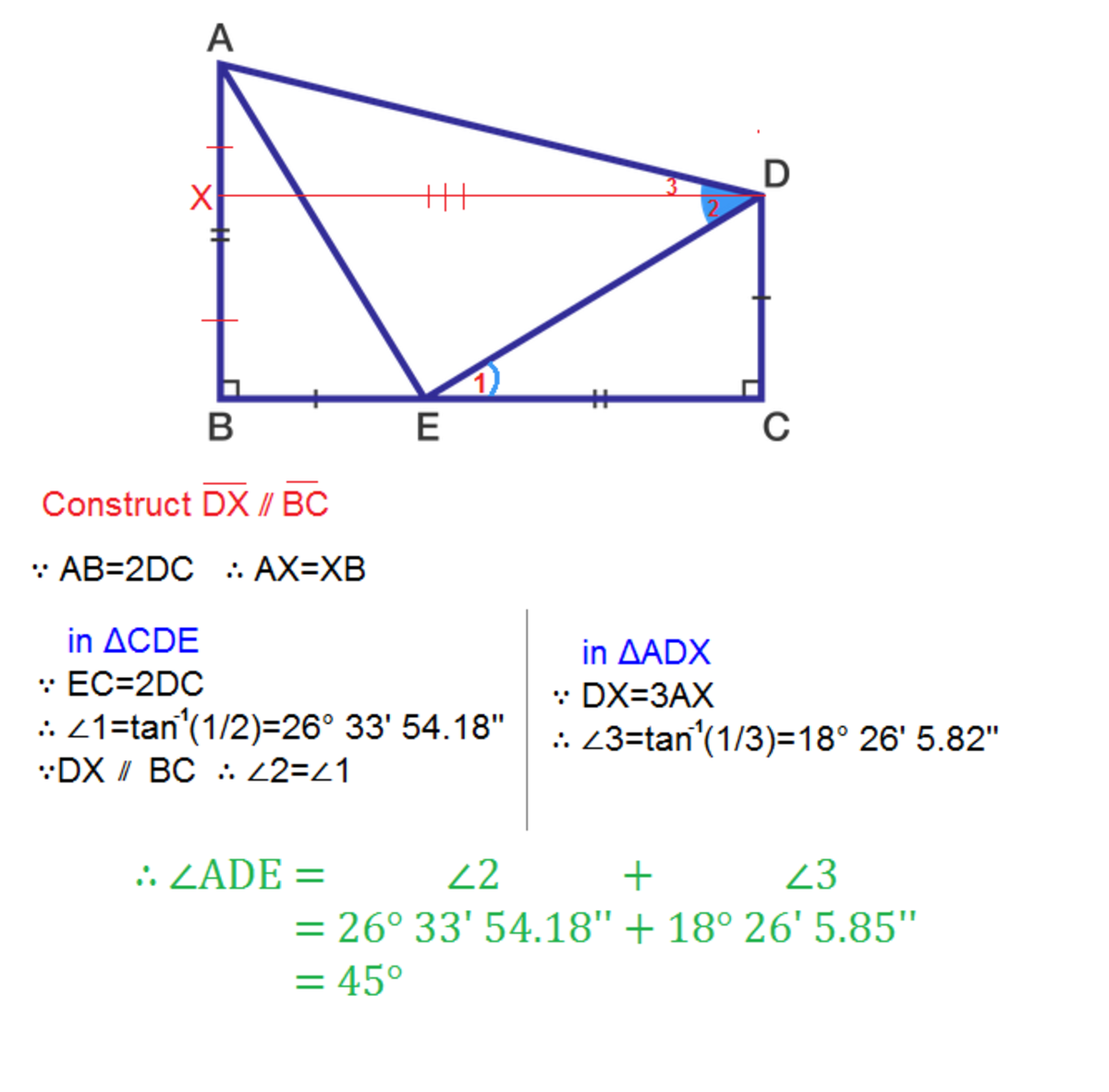
We have from D C ˉ = E B ˉ & A B ˉ = E C ˉ four results ∠ C D E = ∠ B E A ⟹ ( 1 ) ∠ C E D = ∠ B A E ⟹ ( 2 ) ∠ C E D + ∠ C D E = 9 0 ⟹ ( 3 ) A E ˉ = D E ˉ ⟹ ( 4 ) And ∠ C E D + ∠ D E A + ∠ B E A = 1 8 0 So from ( 1 ) & ( 2 ) & ( 3 ) we get ∠ D E A = 9 0 Now we will use ( 4 ) to finish the problem And get ∠ E D A = 4 5
Nice problem keep posting. Wating for one more difficult ; )