What is the measure of the diameter?
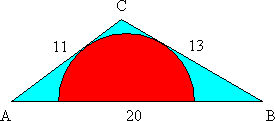
In , side , , and .
Find the diameter of the semicircle inscribed in , whose diameter lies on , and that is tangent to and .
The answer is 11.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
From the tangent points we draw the radii to the center of the circle O which lies on segment AB, then we divide △ A B C into two smaller triangles △ A O C and △ B O C . The sum of the small triangles areas is equal to the area of △ A B C . Let the length of the radius be r , then
[ A O C ] = 2 1 1 r , and
[ B O C ] = 2 1 3 r
Further, from Heron's formula, we can compute the area of △ A B C . The semi-perimeter s = 2 1 ( 2 0 + 1 1 + 1 3 ) = 2 2 . Hence
[ A B C ] = s ( s − a ) ( s − b ) ( s − c ) = ( 2 2 ) ( 2 ) ( 1 1 ) ( 9 ) = ( 1 1 ) ( 2 ) ( 3 ) = 6 6
Thus, 2 1 1 r + 2 1 3 r = 6 6 . Solving for r , we get r = 1 2 6 6 = 2 1 1 .
Therefore, the diameter d = 2 r = 1 1