What is the missing angle?

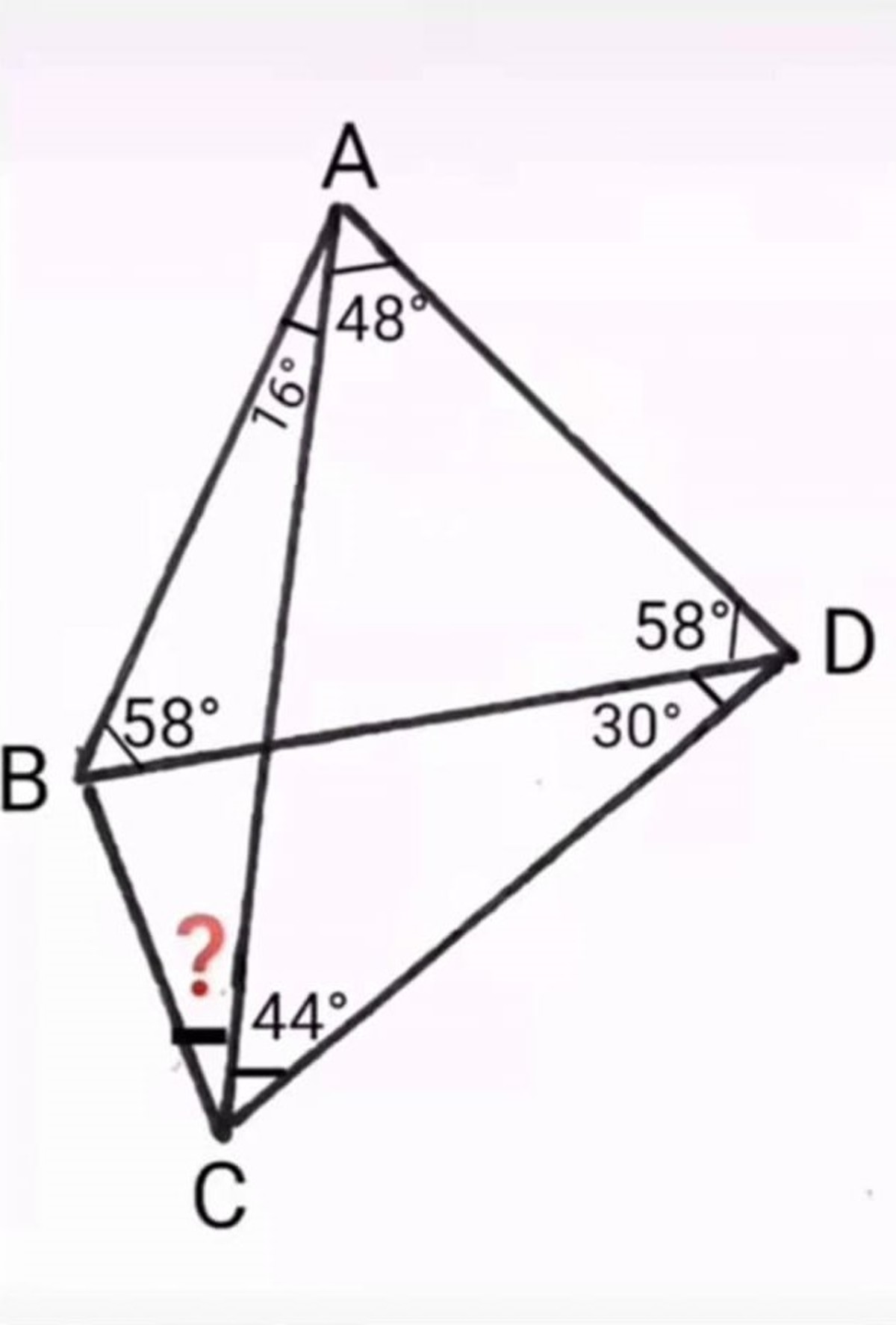
I will show that for any convex quadrilateral the following equations holds true:

$\dfrac{\sin(A)}{\sin(T-A)} \dfrac{\sin(B)}{\sin(T+B)} \dfrac{\sin(C)}{\sin(T-C)} \dfrac{\sin(D)}{\sin(T+D)} =1$

where

$T-A=\angle ABD$ $180-( T+B)=\angle BCA$ $T-C=\angle CDB$ $180-(T+D)=\angle CAD$

$\dfrac{\sin(A)}{\sin(T-A)} \dfrac{\sin(B)}{\sin(180-T-B)} \dfrac{\sin(C)}{\sin(T-C)} \dfrac{\sin(D)}{\sin(180-T-D)} =$

$= \dfrac{\sin(A)}{\sin(T-A)} \dfrac{\sin(B)}{\sin(T+B)} \dfrac{\sin(C)}{\sin(T-C)} \dfrac{\sin(D)}{\sin(T+D)} =$

(Applying sine law for all inner triangles we get)

$= \dfrac{b}{a} \dfrac{c}{b} \dfrac{d}{c} \dfrac{a}{d} = 1$

In our case $\dfrac{\sin(58)}{\sin(16)} \dfrac{\sin(48)}{\sin(58)} \dfrac{\sin(30)}{\sin(44)} \dfrac{\sin(x)}{\sin(74+x)} =1$

This gives the result of $x=30$

Note: This is sort of a variation on the Trigonometric Form of Ceva's Theorem for triangles.