Wow! Large Number!

Logic Level 4

$\large\begin{array}{llllllll}&&&&A&B&C&D\\\times&&&&D&C&B&A\\\hline&5&C&C&B&A&A&D\end{array}$

What is the value of $\overline{DCBA}-\overline{ABCD}$ ?

Clarification : $A,B,C$ and $D$ are distinct single digits with $A$ and $D$ non-zero.

The answer is 3087.

5 solutions

Justine Allen Arciga
Jun 1, 2015

We know that A = 1, since A x D = D.

From the second column we can get C + BD = 11 since C + BD = A and C + BD < 18. pairs with sum 11 are, (11,0) (10,1) (9,2) (8,3) (7,4) (6,5). We can cross out (11,0) (10,1) (9,2) (7,4). That leaves us (8,3) and (6,5).

Values of C,B,D may be (3,4,2) , (3,2,4) , (5,3,2) , (5,2,3).

From the third column, 1 + B + BC + CD = _A. 1 + B + BC + CD < 27 so its value is either 21, 11. Trying the values left from the second column:

(3,4,2) 1 + 4 + 12 + 6 = 23

(3,2,4) 1 + 2 + 6 + 12 = 21

(5,3,2) 1 + 3 + 15 + 10 = 29

(5,2,3) 1 + 2 + 10 + 15 = 28

The only value that's either 11 or 21 is (3,2,4). The answer is A = 1, B = 2, C = 3, D = 4. And if you checked, 1234 x 4321 = 5332114.

$DCBA - ABCD = 4321 - 1234 = \boxed {3087}$

one doubt why C+BD=11 AND C+BD=A in second row of your solution if a=1 b=6 c=9 and d=7 still second column is satisfies can you explain properly.

ojas dhiman - 4 years, 11 months ago

Anonymous1 Assassin
Jan 19, 2021

I used code to solve this:

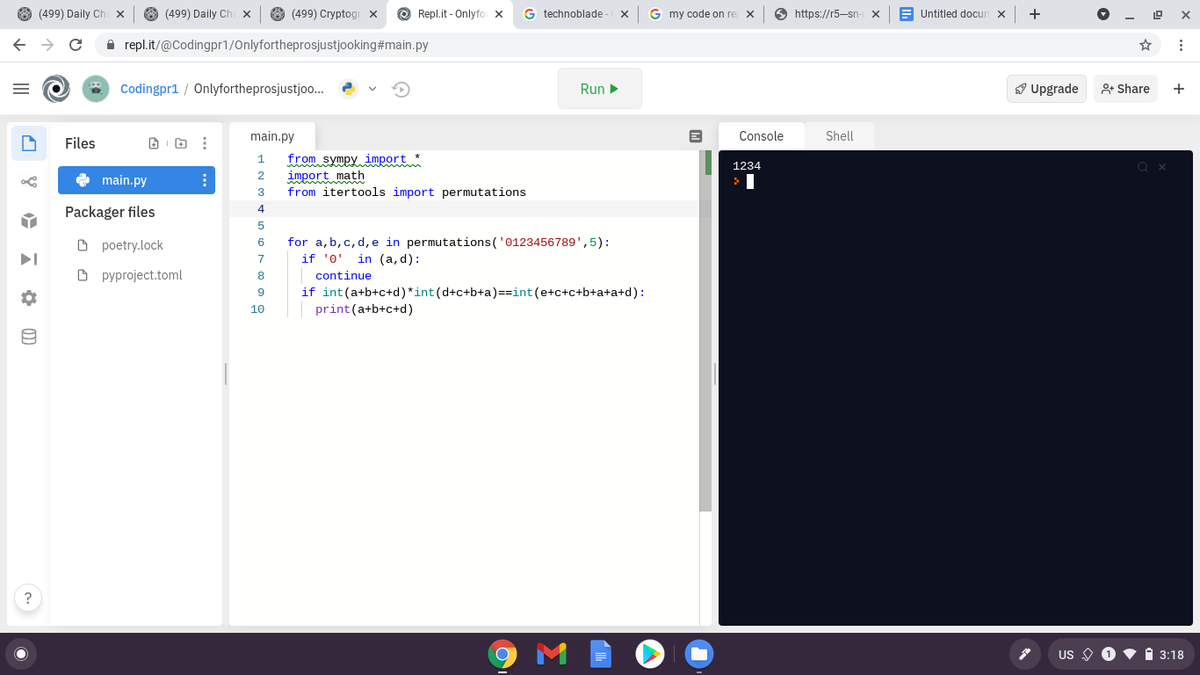
As you can see, even without the 5 (represented by the variable 'e'), we can find the values for a,b,c and d.

Tijmen Veltman
Aug 27, 2015

The Brilliant scratchpad had me doubting my sanity for a while:

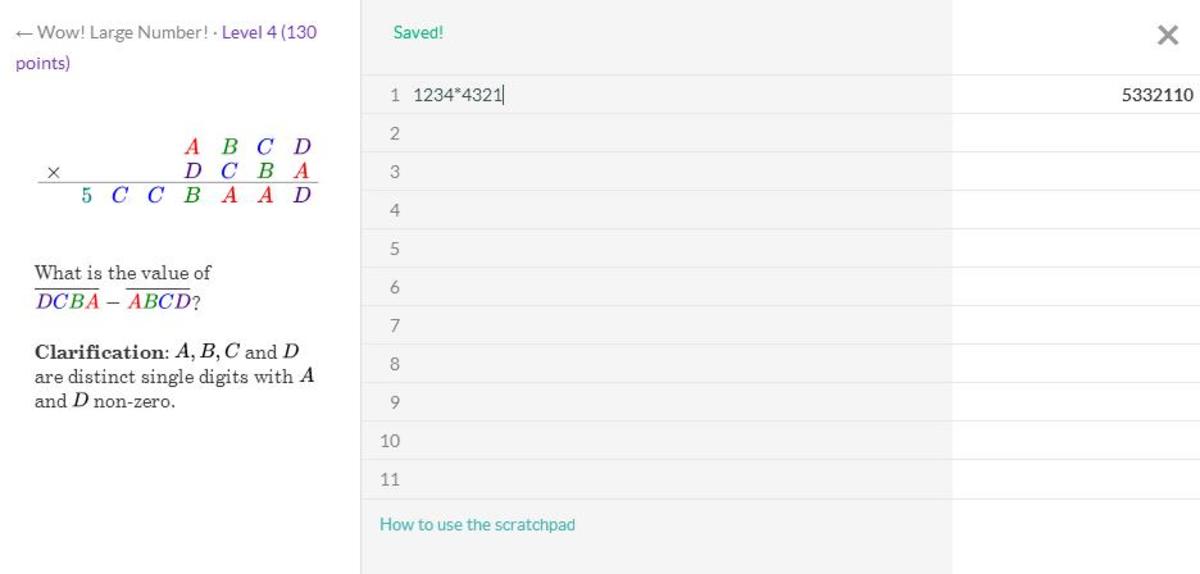
Apparently it always rounds to 6 significant digits. I learned something today.

Shobhit Bhatt
Jun 1, 2015

A=1;B=2;C=3;D=4; ABCD×DCBA=5332114=5CCBAAD, therefore,DCBA-ABCD= 4321-1234=3087

Koushik Kumar
May 31, 2015

So, 4321-1234 =3087

Wow! Large Number!

The answer is 3087.

5 solutions

0 pending reports