What is the Point?
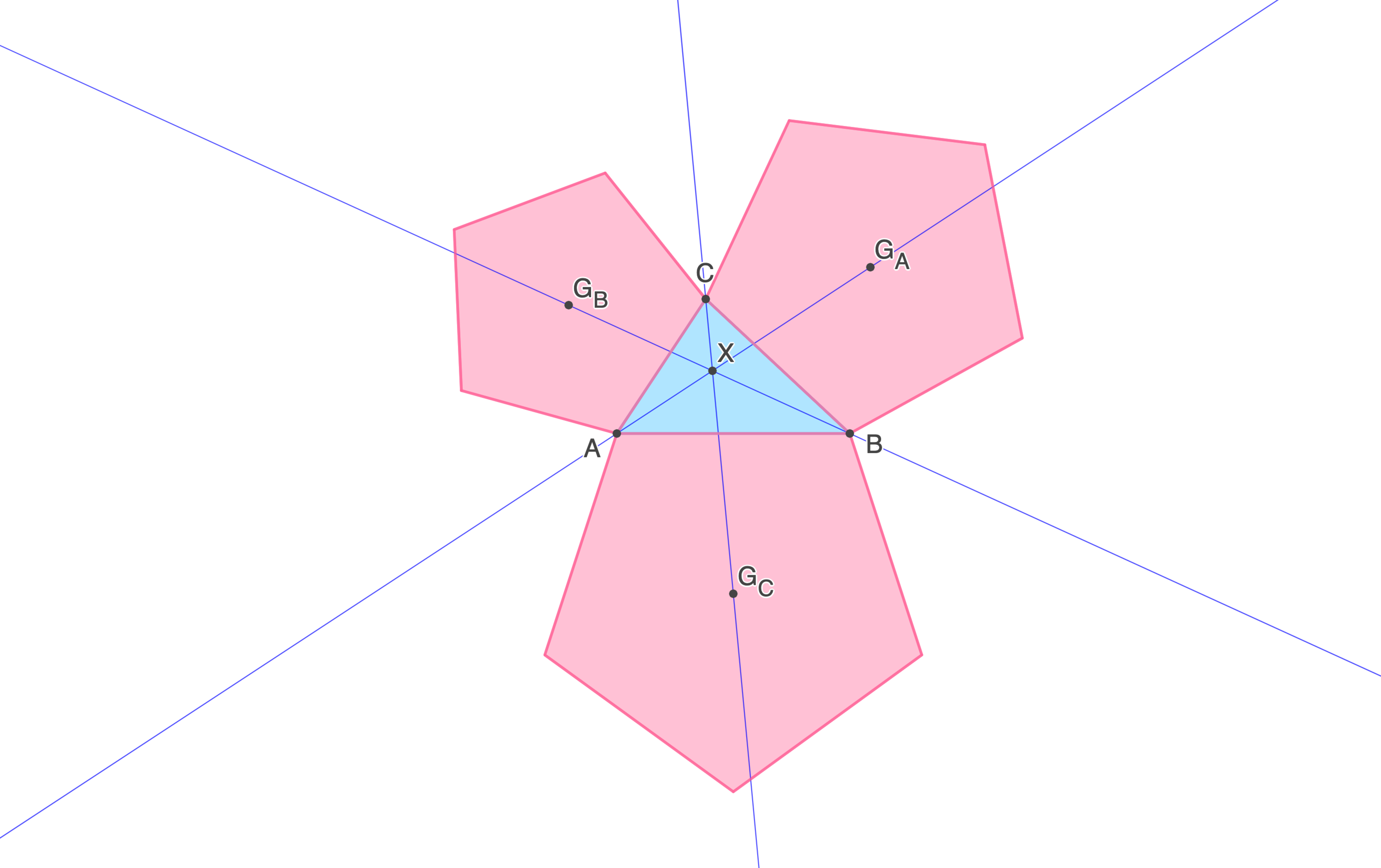
For this problem, let be referred to as the reference triangle. Draw a regular pentagon adjoined to each side of the reference triangle, with pentagon side equal in length to the triangle side, as shown in the figure. Let and be the centroids of the pentagons. Draw lines between and , and , and and . These three lines are concurrent at point . Is a triangle center of the reference triangle, as defined in the Encyclopedia of Triangle Centers (ETC)? If so, what is its number? For example, if it were the incenter, it would be listed in the ETC as , and 1 would be the answer to this problem. If it is not listed in the ETC, enter 0 as the answer.
The answer is 3381.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Given a reference triangle A B C , construct similar isosceles triangles A ′ B C , B ′ A C and C ′ A B externally with the edges B C , A C and A B as respective bases, where the base angle of these isosceles triangles is θ . Then the lines A A ′ , B B ′ , C C ′ are concurrent at the point with trilinear coordinates csc ( A + θ ) : csc ( B + θ ) : csc ( C + θ ) When θ = 0 , we obtain the centroid X ( 2 ) . When θ = 6 1 π , we have the first Napoleon point X ( 1 7 ) . When θ = 2 1 π , we obtain the orthocentre X ( 4 ) . As θ varies, all these points lie on the so-called Kiepert hyperbola .
Constructing a regular pentagon externally on the side of a triangle, and finding its centroid, is essentially constructing an isosceles triangle with base angle θ = 2 1 π − 5 1 π , and so this problem is concerned with the point with triangle center function csc ( A + 2 1 π − 5 1 π ) = sec ( 5 1 π − A ) = sec ( A − 5 1 π ) While the Encyclopedia for Triangle Centers cannot, obviously, list the uncountably infinite number of points that lie on the Kiepert hyperbola, it does list the so-called sec ( A − 5 1 π ) point X ( 3 3 8 1 ) . For those with access to Geometer's Sketchpad, here is a visualisation of this triangle centre.