What is the rise in the water level?

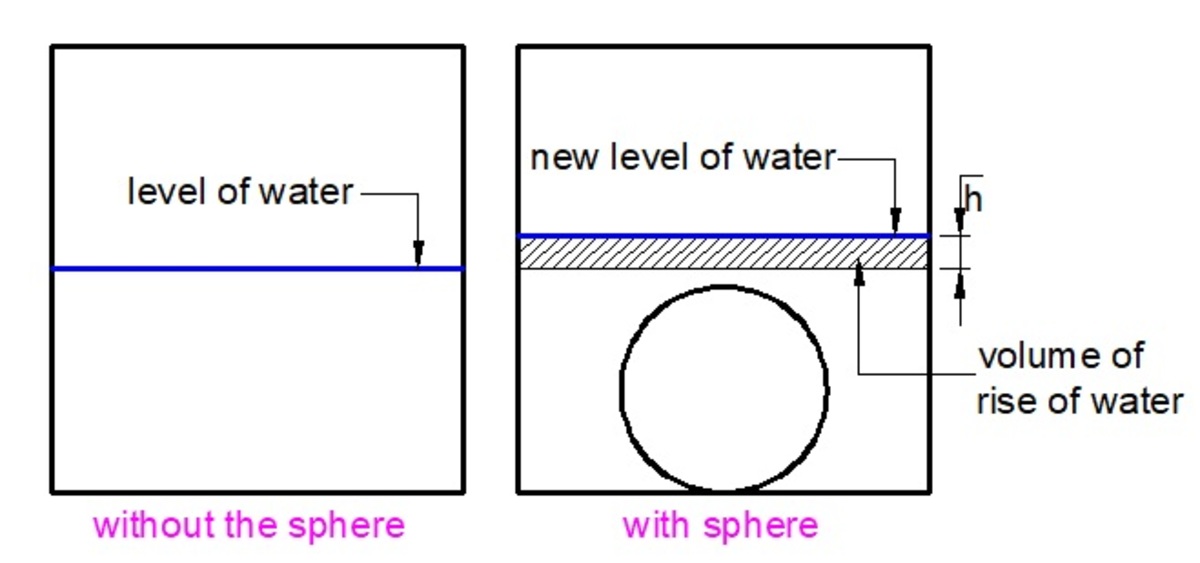
The sphere has a diameter of 6 cm. That means its radius is 3 cm. The volume of a sphere is determined by the formula

$V_{sphere} = \frac {4}{3} \pi r^3$

Applying the known values, we get $36\pi \mathrm{cm}^3$

Now we have to determine the base area of the cylinder. This can be determined by the formula for the area of a circle:

$A_{circle} = 2\pi r$

Applying the known values, we get $36\pi \mathrm{cm}^2$ .

Since the sphere was dropped into the cylinder, the rise in water level (due to displacement) is equivalent to the $Volume_{object}$ divided by the $Volume_{measurer}$ . In this case, it would simply be

$\frac {36}{36}$

or simply $1$ . Now we know that the water rose by 1 cm.

Consider the diagram on the left.

The volume of the sphere is equal to the volume of rise of water. So we have

$\dfrac{4}{3} \pi (3^3)=\pi (6^2)(h)$

$36=36h$

$\boxed{h=1}$