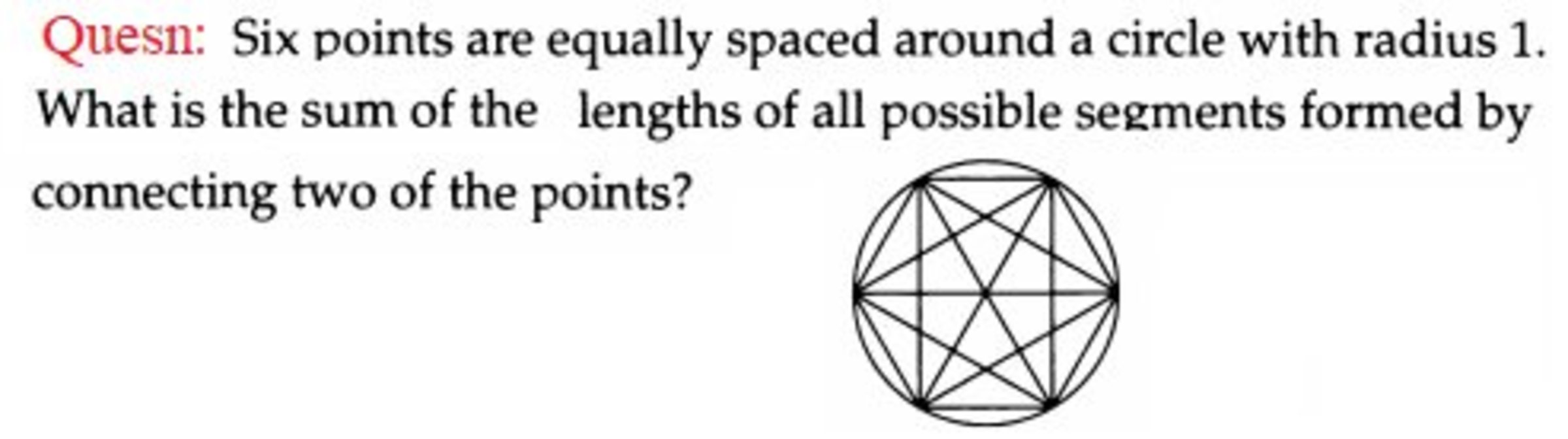
WHAT IS THE SUM OF ALL POSSIBLE SEGMENTS FORMED BY JOINING 2 POINTS?(radius=1)

ANS: 6+3x2+6 root 2 . See 6 sides of length 1, three diagonals of length 2 and six diagonals of length root 3. Thus the answer will come.

Direct computation:

$p=\text{Table}\left[\{\cos (\theta ),\sin (\theta )\},\left\{\theta ,0,\frac{5 \pi }{3},\frac{\pi }{3}\right\}\right]$

$\frac{1}{2} \text{Total}[\text{Flatten}[\text{Table}[\text{EuclideanDistance}[r,s],\{r,p\},\{s,p\}]]]\Rightarrow 6 \left(\sqrt{3}+2\right)$

The reason for the division by 2 is that everything is included twice, including the zero length segments or a point to itself, which do not change the answer. Doing it this way simplified the loop coding.