What is the Transition Matrix?

Probability Level 1

A Markov chain has first state A and second state B, and its transition probabilities for all time are given by the following graph:

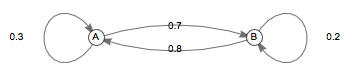
What is its transition matrix ?

Note: The transition matrix is oriented such that the k th k^\text{th} row represents the set of probabilities of transitioning from state k k to another state.

( 0.3 0.8 0.7 0.2 ) \begin{pmatrix} 0.3 & 0.8 \\ 0.7 & 0.2 \end{pmatrix} ( 1 0.8 0.7 1 ) \begin{pmatrix} 1 & 0.8 \\ 0.7 & 1 \end{pmatrix} ( 0.5 1.5 1.5 0.5 ) \begin{pmatrix} 0.5 & 1.5 \\ 1.5 & 0.5 \end{pmatrix} ( 0.3 0.7 0.8 0.2 ) \begin{pmatrix} 0.3 & 0.7 \\ 0.8 & 0.2 \end{pmatrix}

View wiki
Henry Maltby by Henry Maltby , 26, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

Henry Maltby
Apr 28, 2016

Relevant wiki: Markov Chains

Recall that the ( i , j ) th (i, \,j)^\text{th} entry of the transition matrix is Prob ( X n + 1 = j ∣ X n = i ) \text{Prob}(X_{n+1} = j \mid X_n = i) . Therefore, the rows each represent the outgoing arrows from a given vertex, and the answer is ( 0.3 0.7 0.8 0.2 ) . \boxed{\begin{pmatrix} 0.3 & 0.7 \\ 0.8 & 0.2 \end{pmatrix}.}

13 Helpful 3 Interesting 0 Brilliant 1 Confused

Since the total of transition probability from a state i i to all other states must be 1 1 , then

∑ j Pr ⁡ [ X n + 1 = j ∣ X n = i ] = 1. \sum_j \Pr\left[X_{n+1}=j\left|\right.X_{n}=i\right]=1.

The only possible answer is option 2.

Tunk-Fey Ariawan - 5 years, 1 month ago

Hey, you have to be careful there. There are two ways of handling with Matrices, since you can transpone a matrix, so that the rows and columns are exchanged.

Sandra gajic - 2 years, 1 month ago
Ash Gray
Nov 21, 2019

Parsing through the terse math we were given, it boils down to the explanation that for any state i the probability of transitioning to state j is given by the entry in the transition matrix at position i,j. Given that i indicates the row and j the column, we assume that a is the 0th position and b the 1st, so the transition probability from A to A is .3, A to B is .7, B to A is .8 and B to B is .2; therefore the correct matrix is ( . 3 . 7 . 8 . 2 ) \begin{pmatrix} .3 & .7 \\ .8 & .2 \end{pmatrix} .

5 Helpful 0 Interesting 0 Brilliant 0 Confused
Shekhar Koirala
Sep 30, 2018

( 0.65 0.35 ) ( 0.4 0.6 )

2 Helpful 1 Interesting 0 Brilliant 3 Confused

It's a trick question. The question asks for the Transition Matrix, not the 2 Step Matrix as demonstrated in the text above the question.

Andrew Aaron - 1 year, 5 months ago

1 pending report

Vote up reports you agree with

×

Problem Loading...

Note Loading...

Set Loading...