What is the volume of this shape?

Calculus Level 3

${\color{#D61F06}\text{This problem's question:}}$ What is the volume of this shape?

This problem, since only a numeric answer is needed, is most easily solved by a numeric integration.

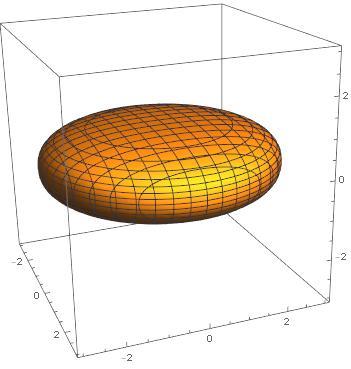
The formula for the shape: $0.0641500299099584 \left| x^2+y^2\right| ^{1.25}+\left| z\right| ^{2.5}\leq 1$ .

The accuracy of the first numeric value is far in excess of what is needed. Use as much as you think you need.

The answer is 42.4131047962912.

2 solutions

D G
Jun 18, 2019

Let $a = 0.0641500299099584$ . We can rewrite the equation as

$|x^2 + y^2| \leq \left(\frac{1 - |z|^{5/2}}{a}\right)^{4/5}$

This is just a circle in the x-y plane. Our volume is then

$2 \int_{0}^{1} \frac{\pi \left(1 - z^{\frac{5}{2}}\right)^{\frac{4}{5}}}{a^{\frac{4}{5}}}\, dz = \frac{4 \cdot 2^{\frac{2}{5}} \sqrt{\pi} \Gamma\left(\frac{7}{10}\right) \Gamma\left(\frac{4}{5}\right)}{3 a^{\frac{4}{5}}}$

Substitute the value of $a$ to get the final result.

Thank you.

The original form of $a$ is $\frac{1}{9\sqrt{3}}$ .

With the original form of $a$ and using the methodology you apparently used, I came to dissimilar looking solution, but mathematically the same: $-\frac{18 \sqrt{2+\frac{2}{\sqrt{5}}} \pi ^2 \Gamma \left(\frac{7}{5}\right)}{\Gamma \left(-\frac{4}{5}\right) \Gamma \left(\frac{11}{5}\right)}$ .

I have registered a problem report (4272791) with Wolfram. Numerically, the answer to the problem is too dissimilar to the correct answer. The numeric answer to the symbolic form is 42.4131047962912.

I now see that Wolfram/Alpha returns your form of the definite integral (after moving outside the integration the constant terms): $\int_0^1 \left(1-z^{5/2}\right)^{4/5} \, dz=\frac{2\ 2^{2/5} \Gamma \left(\frac{7}{10}\right) \Gamma \left(\frac{4}{5}\right)}{3 \sqrt{\pi }}$ .

The indefinite integral is: $\frac{1}{3} z \left(2 \, _2F_1\left(\frac{1}{5},\frac{2}{5};\frac{7}{5};z^{5/2}\right)+\left(1-z^{5/2}\right)^{4/5}\right)$ .

A Former Brilliant Member - 1 year, 11 months ago

A Former Brilliant Member
Jun 18, 2019

$\text{Volume}\left[\text{ImplicitRegion}\left[\text{Evaluate}\left[\left| \frac{z}{h}\right| ^p+\left| \frac{\sqrt{x^2+y^2}}{r}\right| ^p\text{/.}\, \{p\to 2.5,r\to 3.,h\to 1.\}\right]\leq 1, \\ \left( \begin{array}{ccc} x & -3 & 3 \\ y & -3 & 3 \\ z & -3 & 3 \\ \end{array} \right)\right]\right] \Rightarrow 42.0705845239179$

Please, see my comments on D G's solution.

What is the volume of this shape?

The answer is 42.4131047962912.

2 solutions

0 pending reports