What Is This Point?
Let △ A B C be an acute angled triangle with side lengths A B = 5 , B C = 7 , C A = 8 . Let D be the foot of perpendicular from A to B C , and let O be its circumcenter. The feet of perpendiculars from O to A B and A C intersect A D at points Q and P respectively. Let S be the circumcenter of △ O P Q . If cos ( ∠ C A S ) = c a b for some square free integer b and coprime positive integers a and b , then find a + b + c .
Details and assumptions
- This problem is adapted from an ARO 10th grade geometry problem.
The answer is 175.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
My solution turns out to be a bit long and operational. As many will have noticed, both triangles are similar. △ O P Q . is similar to △ A C B .
Angle BAC = 60°. We take advantage of the fact that the triangles are similar and we draw a perpendicular OJ to AD.
We find the area of the triangle ABC by Heron's theorem, [ABC]= 1 0 3 .
Then AD = 7 2 0 3
We draw the peperndicular bisector of BC, such that it intersects it at point G; AD = 7 5 , DG = 1 4 3 9 , GC = 2 7 . OGDJ is a rectangle, so OJ = GD = 39/14. We already have the relation of sides that have both triangles, then we draw SI perpendicular to AD. By similarity; SI = 8 0 9 1 , IQ = 8 0 9 1 3 , QA= 2 4 0 6 2 3 3 .
We use composite angle cosine between SAD and CAD to find the cosine of CAS. We can obtain the sine and cosine of CAD by drawing a perpendicular to AC and using the circumradio in the triangle formed.
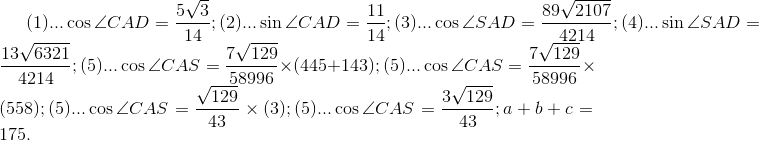
Sorry for the bad english, is the first time I publish a solution.
We shall work with the configuration shown in the diagram throughout the solution. I'm too lazy to check which configuration the given side lengths produce, but the solution for both configurations should be similar. I shall use the following fact without mention in my solution.
Fact: If S is the circumcenter of △ P Q R , ∠ S P Q = 9 0 ∘ − ∠ Q P R .
The proof of this simple fact is left to the reader.
Let K , L , M be the midpoints of A C , A B , B C respectively. Since O M ⊥ B C and O L ⊥ A B , quadrilateral B M O L is cyclic with diameter B O .
Since O M and A D are both perpendicular to B C , O M ∥ A D . Then note that ∠ O Q P = = = 1 8 0 ∘ − ∠ Q O M 1 8 0 ∘ − ( 1 8 0 ∘ − ∠ A B C ) ∠ A B C . Similarly, ∠ O P Q = ∠ A C B . Therefore, triangles △ O P Q and △ A B C are similar, and ∠ P O Q = ∠ B A C . Similar arguments to the first paragraph show that quadrilateral A L O K is also cyclic, so ∠ A O Q = = = ∠ A K L ∠ A C B ∠ Q P O , which implies A O is tangent to the circumcircle of △ O P Q . This gives O A ⊥ S O .
Since D M ⊥ A D , O S ⊥ O A , and A D ∥ O M , D M equals the length of the altitude from O of △ O P Q (if this is not obvious, consider the foot of perpendicular from O to P Q and note that that point forms a rectangle with O , D , M using the aforementioned facts). Since △ O P Q and △ A B C are similar, A D D M = B C P Q . Again, O S and O A are the circumradii of △ O P Q and △ A B C respectively, so O A O S = B C P Q = A D D M . Since ∠ A D C = ∠ A O S = 9 0 ∘ , △ A S O and △ M A D are similar. Consequently, ∠ S A O = ∠ M A D . Finally, ∠ C A S = = = = ∠ C A O + ∠ S A O 9 0 ∘ − ∠ A B C + ∠ M A D ∠ B A D + ∠ M A D ∠ B A M .
It suffices to find cos ∠ B A M . Let A M = x . By Stewart's theorem on △ A B C and cevian A M , we find out that 5 2 + 8 2 = 2 ( x 2 + ( 2 7 ) 2 ) ⟹ x = 2 1 2 9 , and by Cosine rule on △ A B M , cos ∠ B A M = 2 ⋅ 5 x 5 2 + x 2 − ( 2 7 ) 2 = 4 3 3 1 2 9 ,
so a = 3 , b = 1 2 9 , c = 4 3 , and a + b + c = 1 7 5 .