What name shall I give to this problem? - 2
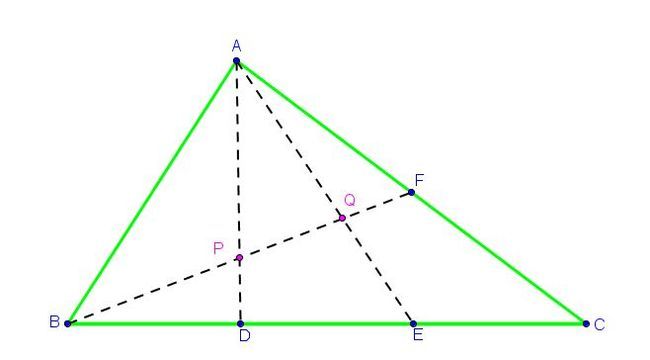 In
△
A
B
C
,
D
and
E
are points on
B
C
such that
B
D
=
D
E
=
E
C
.
F
is a point on
A
C
such that
A
F
=
F
C
. If
A
D
and
A
E
intersect
B
F
respectively at
P
and
Q
. Then, the ratio
P
Q
B
P
can be expressed as
b
a
, where
a
and
b
are coprime integers. Find
1
0
a
+
b
.
In
△
A
B
C
,
D
and
E
are points on
B
C
such that
B
D
=
D
E
=
E
C
.
F
is a point on
A
C
such that
A
F
=
F
C
. If
A
D
and
A
E
intersect
B
F
respectively at
P
and
Q
. Then, the ratio
P
Q
B
P
can be expressed as
b
a
, where
a
and
b
are coprime integers. Find
1
0
a
+
b
.
This problem is from the set What name should I give?
The answer is 53.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Moderator note:
Good approach with using the parallel lines to help determine the ratios via similar figures.
I joined EF and then proceeded
A great and simple approach bro!!!
By Menelaus Theorem of Transversal Line, we need to find the ratio of A Q E A to find the ratio of P Q B P
Thus, we have the A Q E A via the transversality of point B , Q , F B E C B Q A E Q F C A F = 1 2 3 Q A E Q 1 1 = 1 Q A E Q = 3 2
In conclusion, we have A Q E A = 3 5
Then, by finding the ratio of P Q B P , we use the transversality of A , P , D A Q E A P B Q P D E B D = 1 3 5 P B Q P 1 1 = 1 P B Q P = 5 3 P Q B P = 3 5
a = 5 , b = 3 ⇒ 1 0 a + b = 5 3
Yay Menelaus' Theorem !
Yup, same approach bro, up voted !
Very nice!Thanx for helping me understand this concept!
I did not use the theorem, but the same steps!!
Let
 be on line segment
be on line segment
 such that
such that
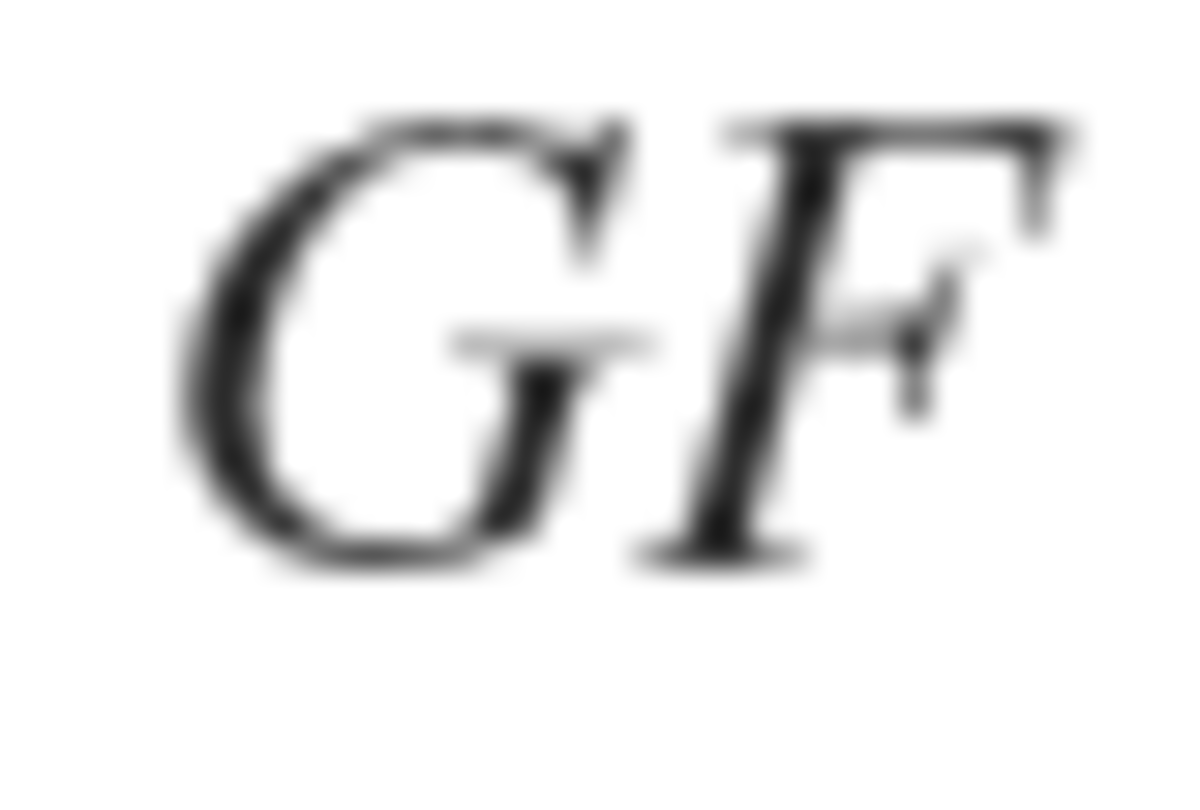 is parallel to
is parallel to
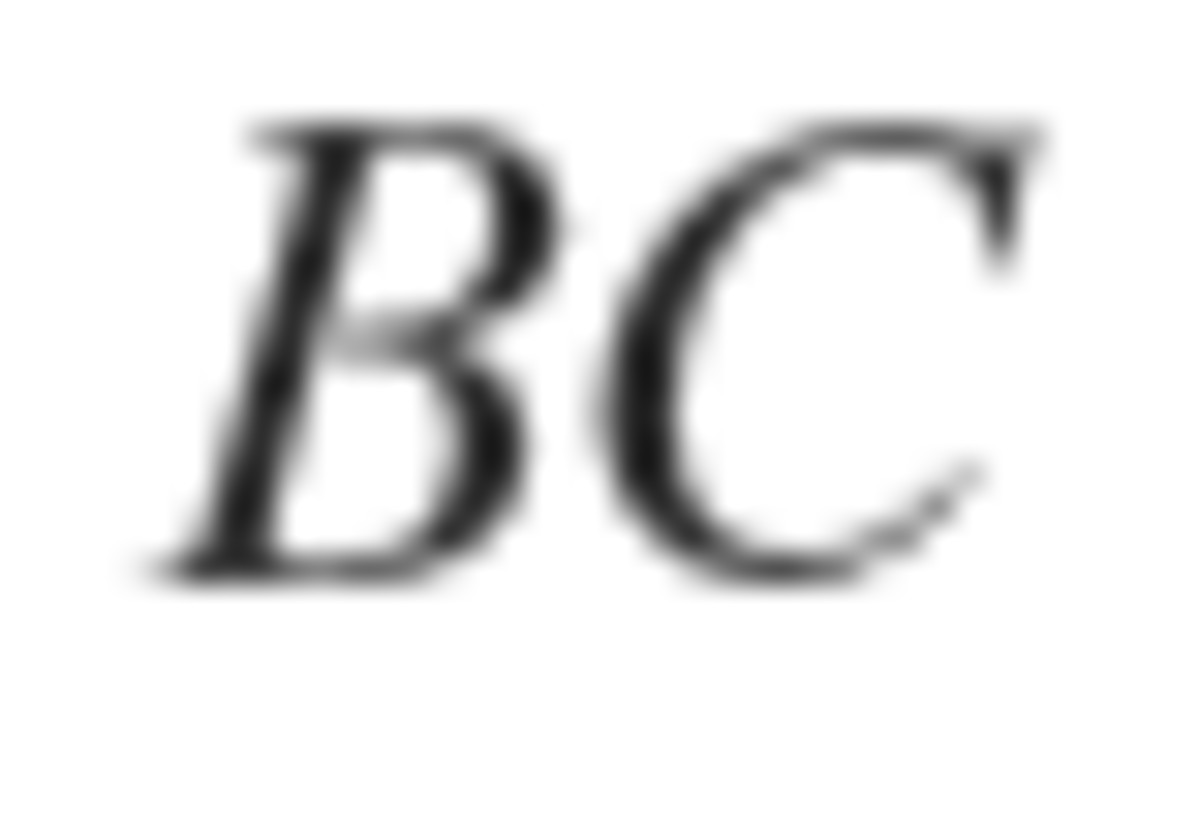
Let
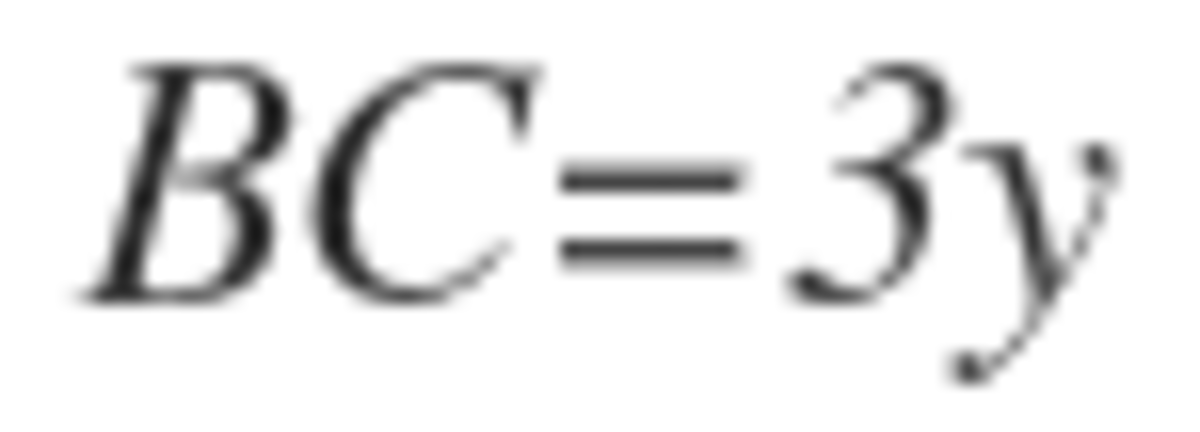 , so therefore
, so therefore
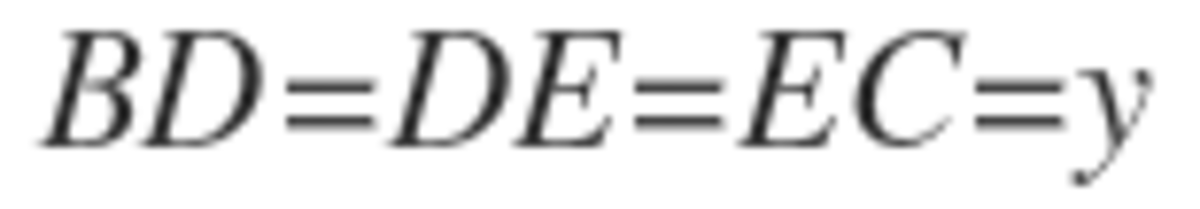
Since
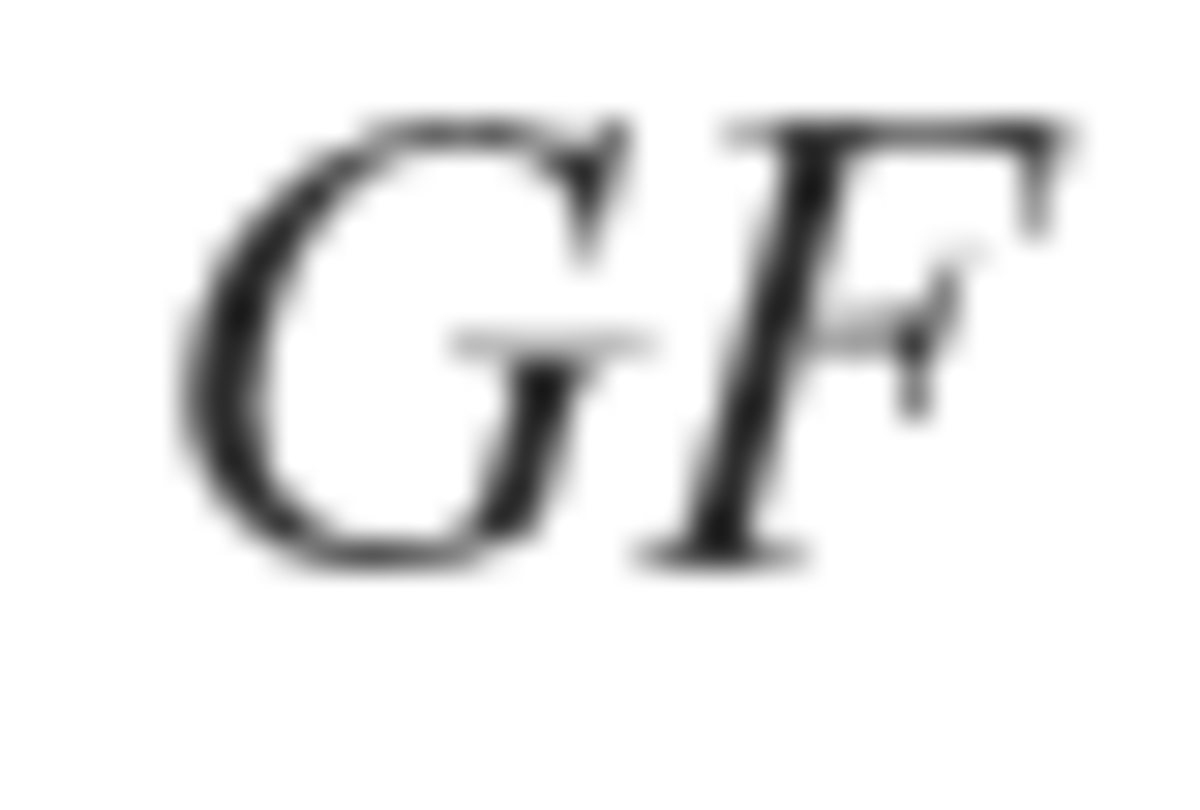 is parallel to
is parallel to
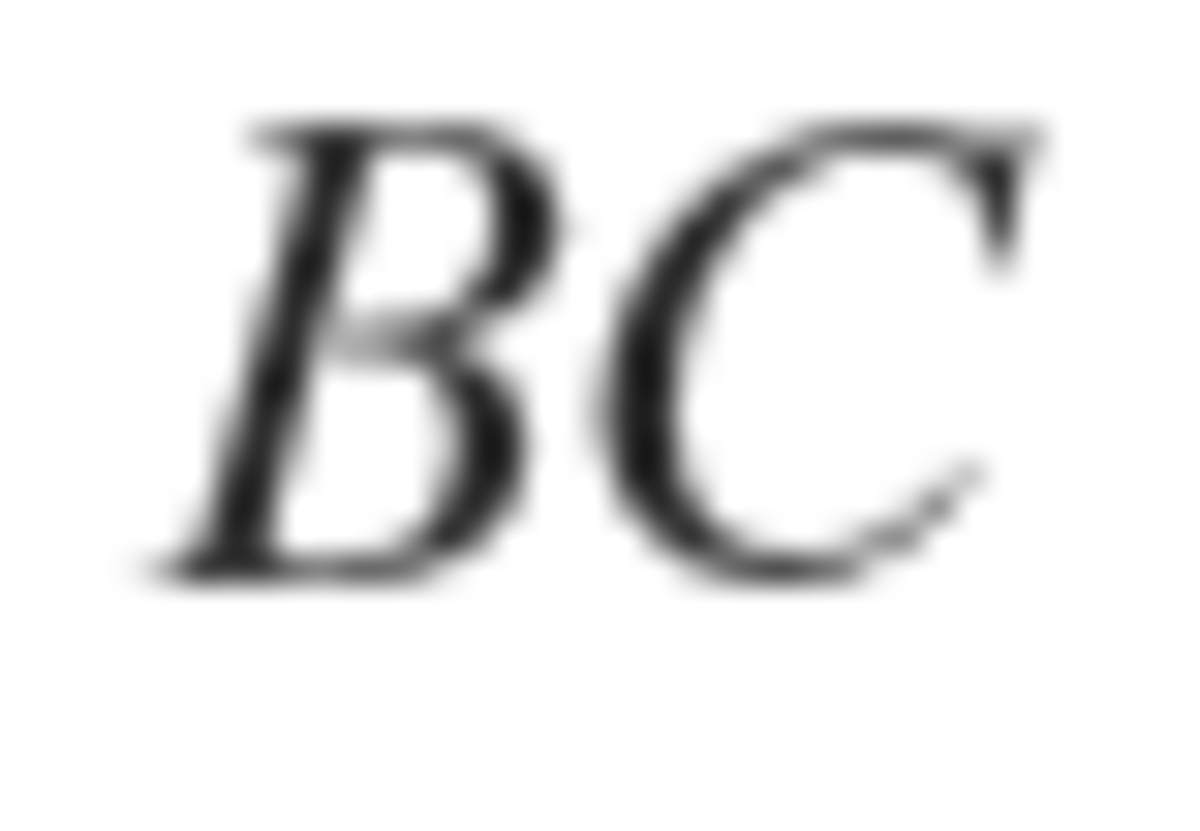 , we know that
, we know that
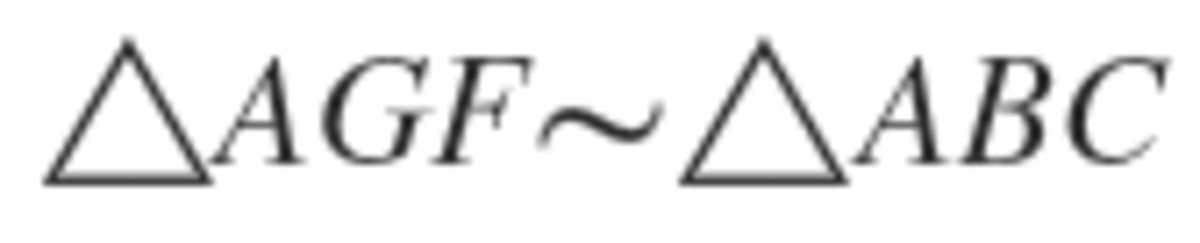 so that means
so that means
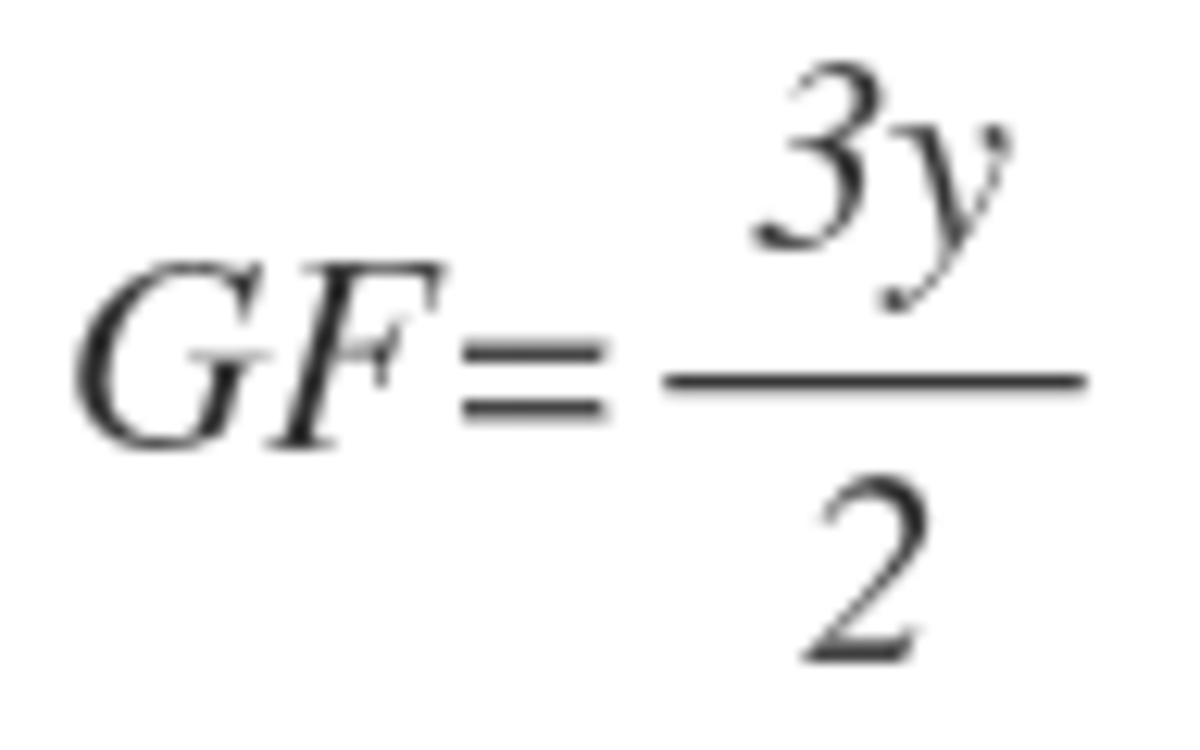
That also leads to more similiar triangles which means
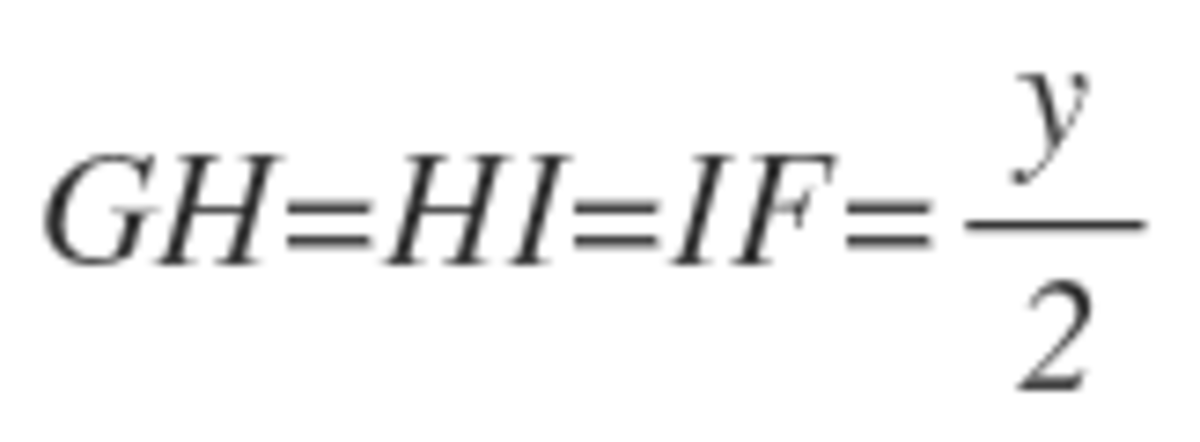
Notice that
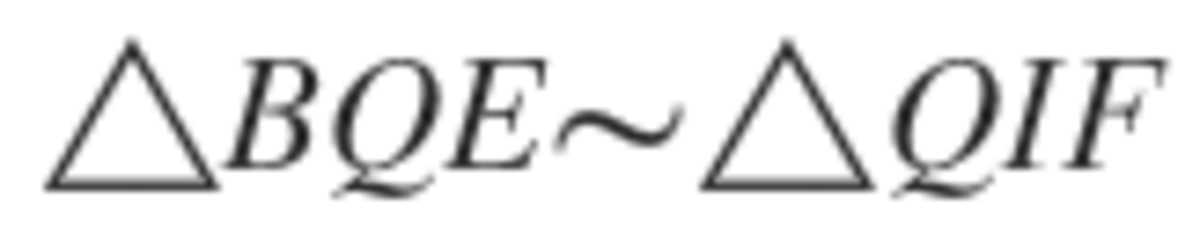 , which means
, which means
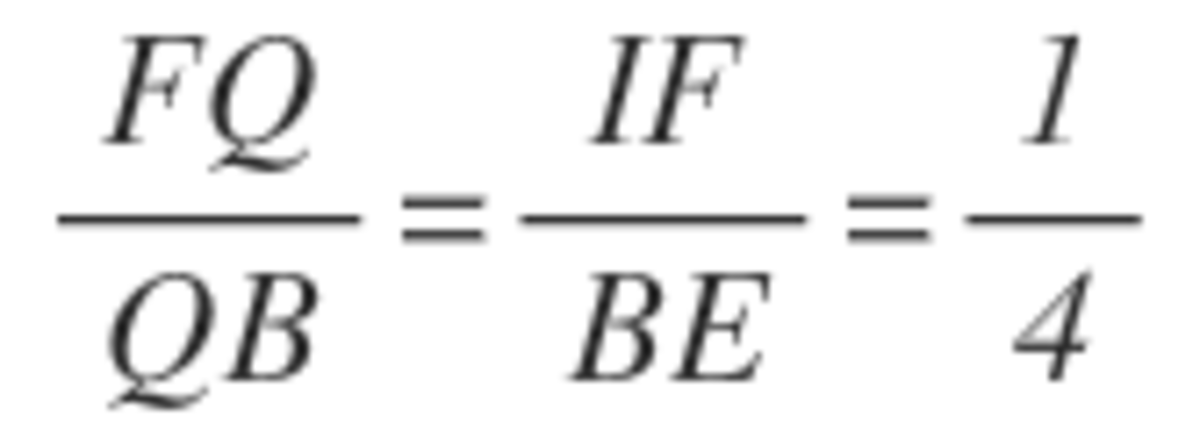
Now let
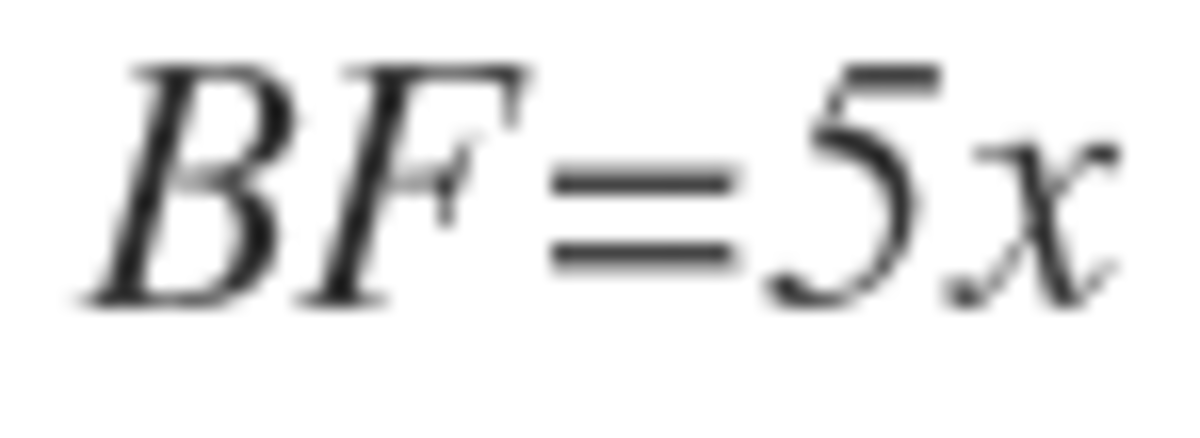 which means
which means
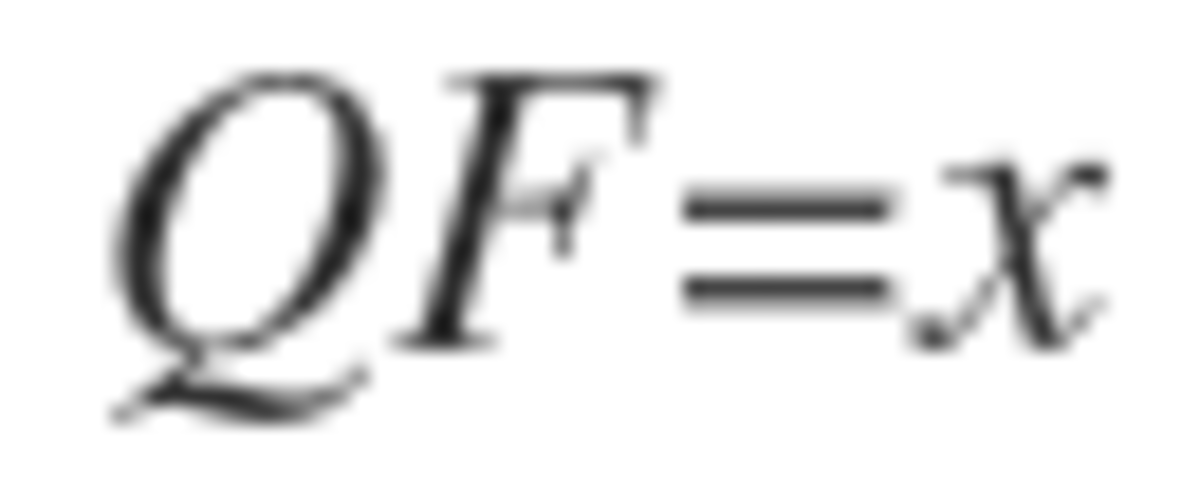 and
and
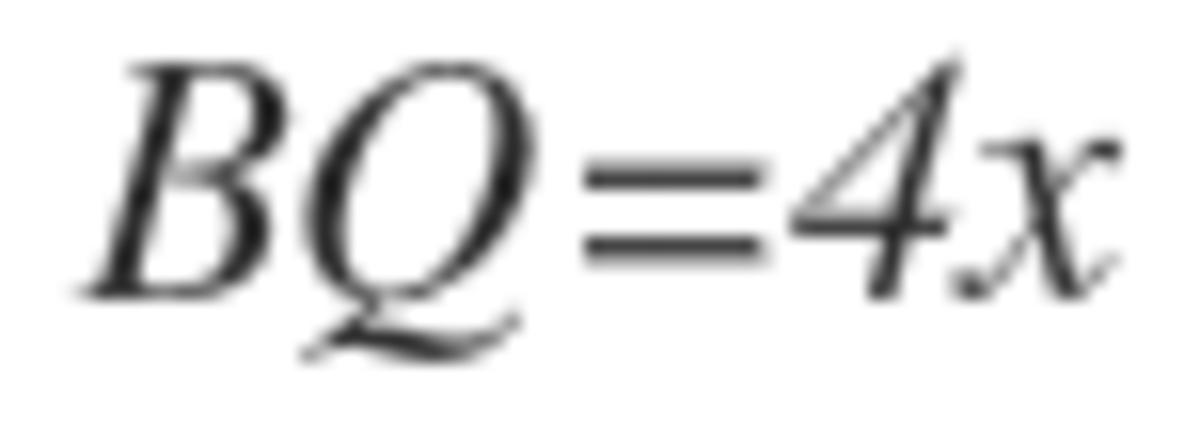
Also we notice
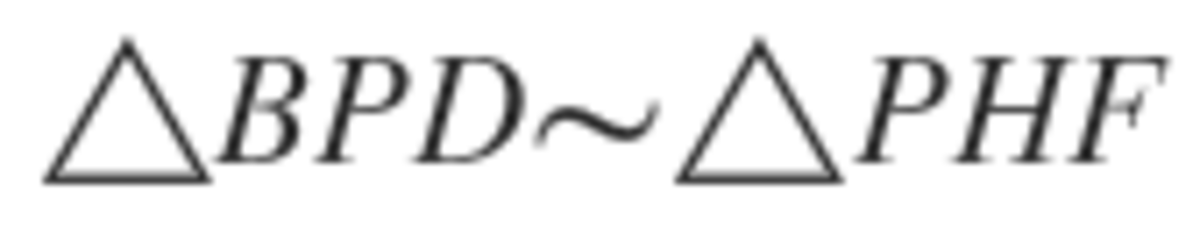 . Because
. Because
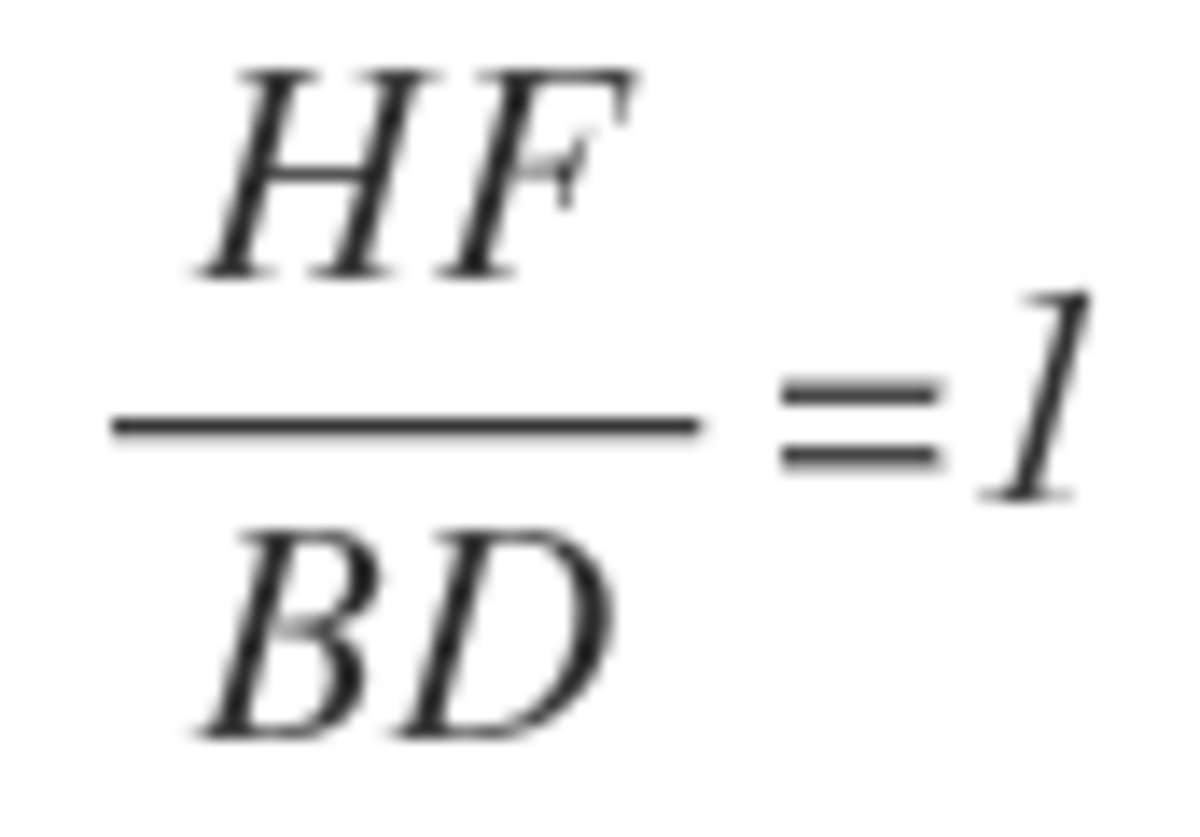 ,
,
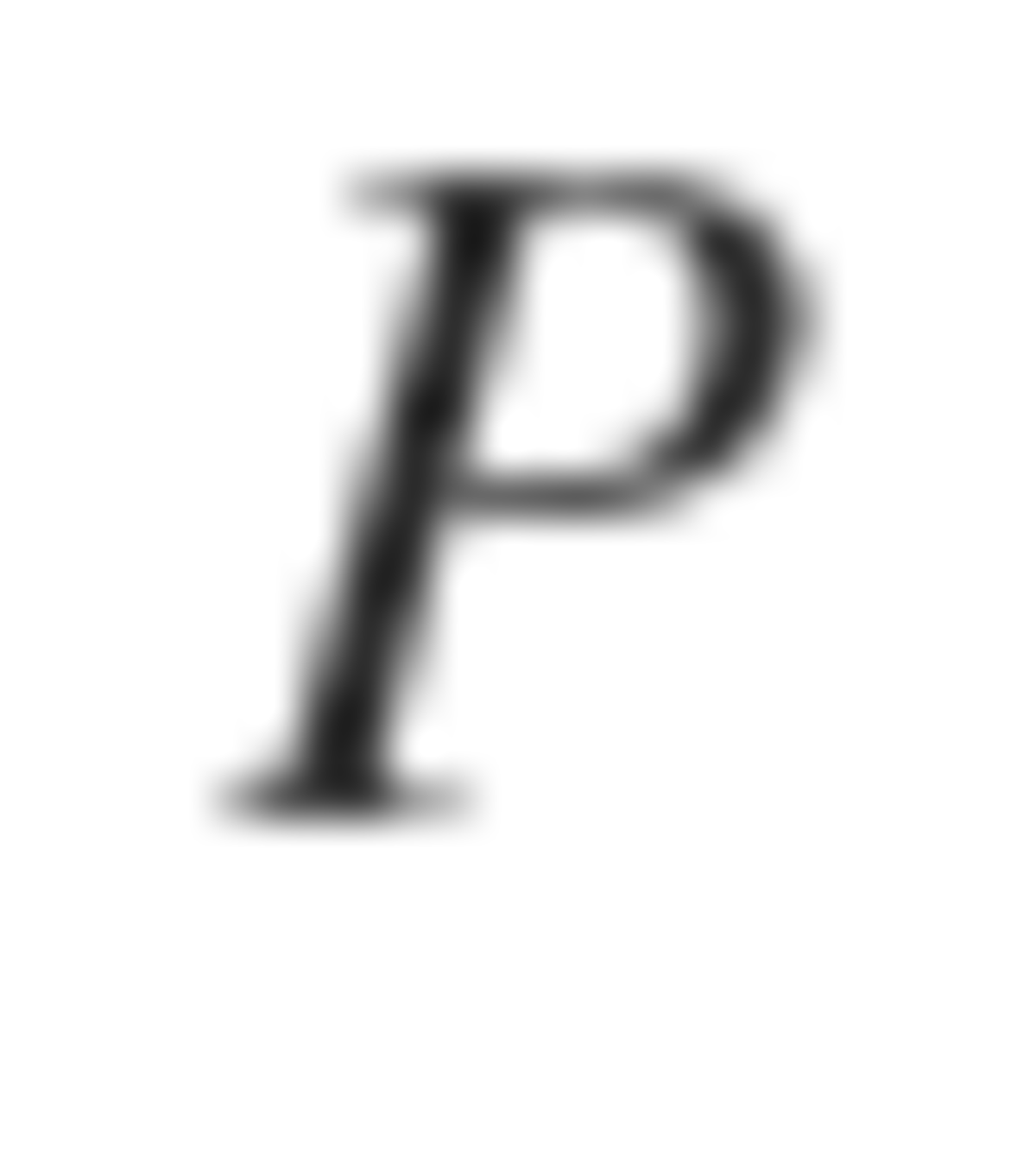 is the midpoint of
is the midpoint of
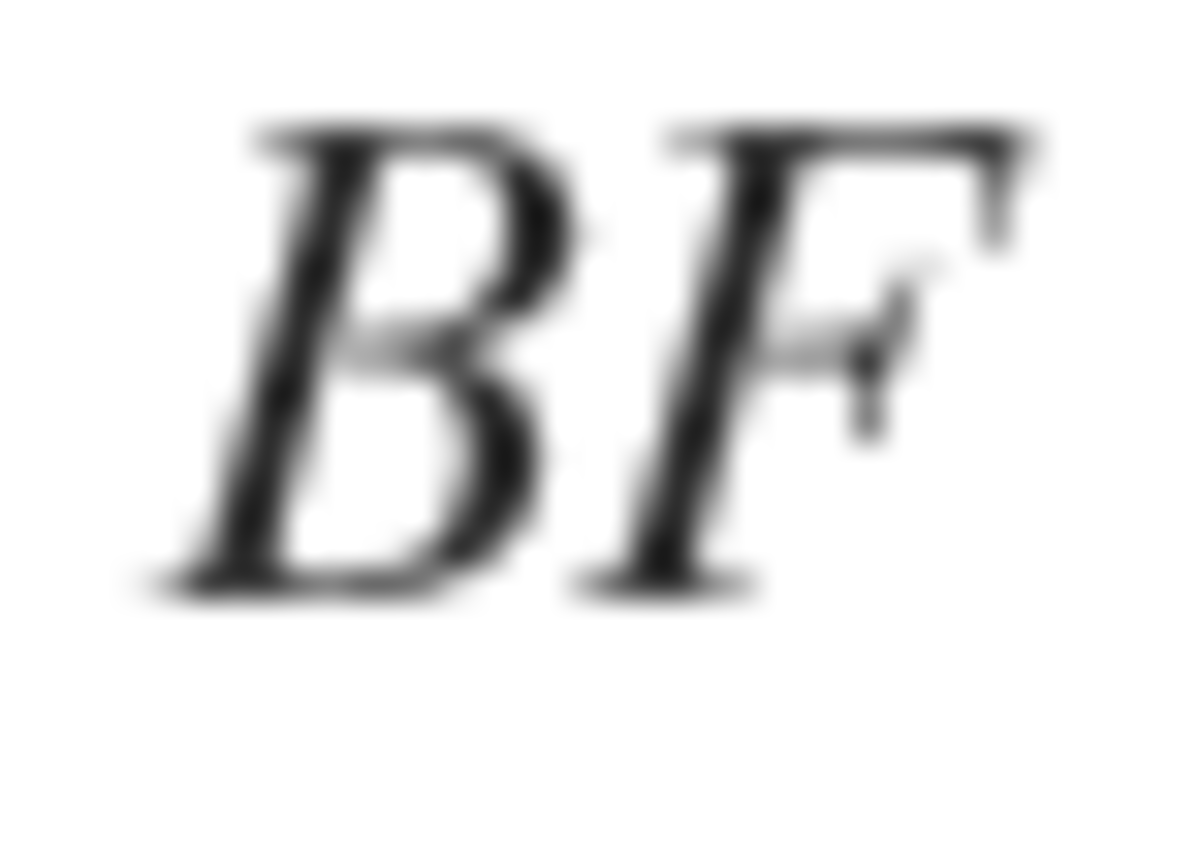 .
.
That means
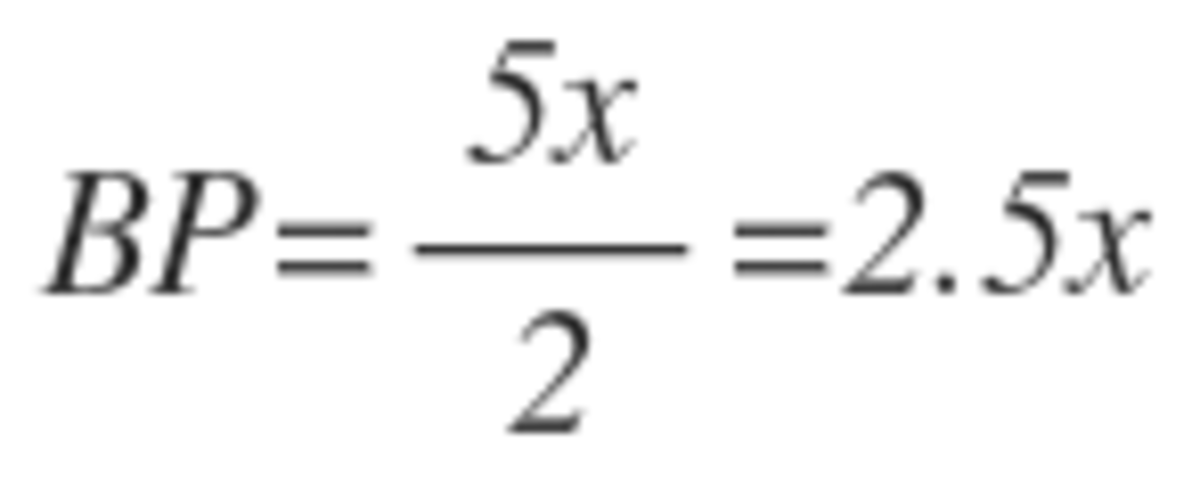 which leaves
which leaves
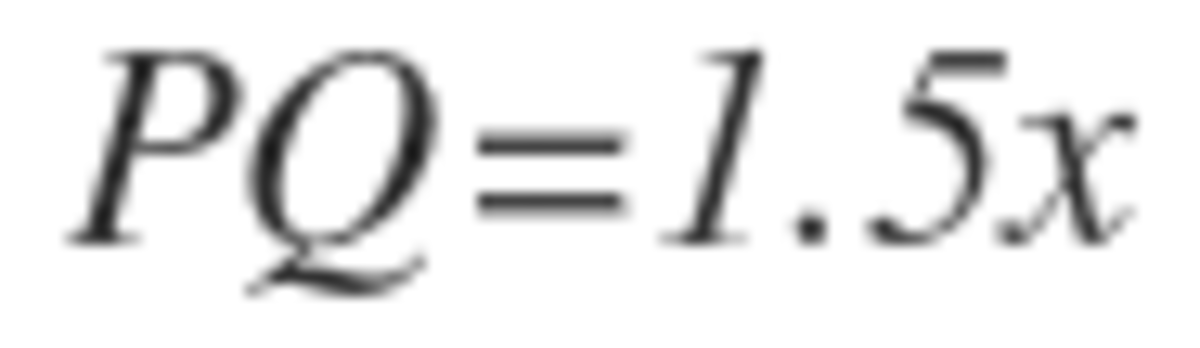

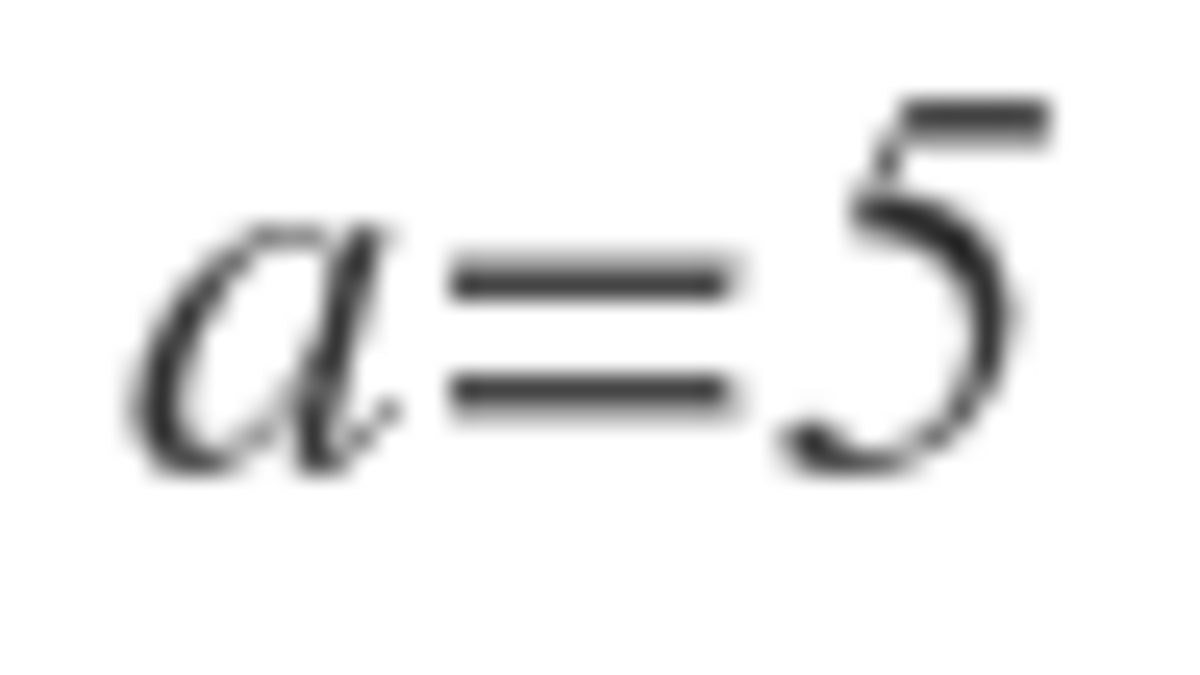 and
and
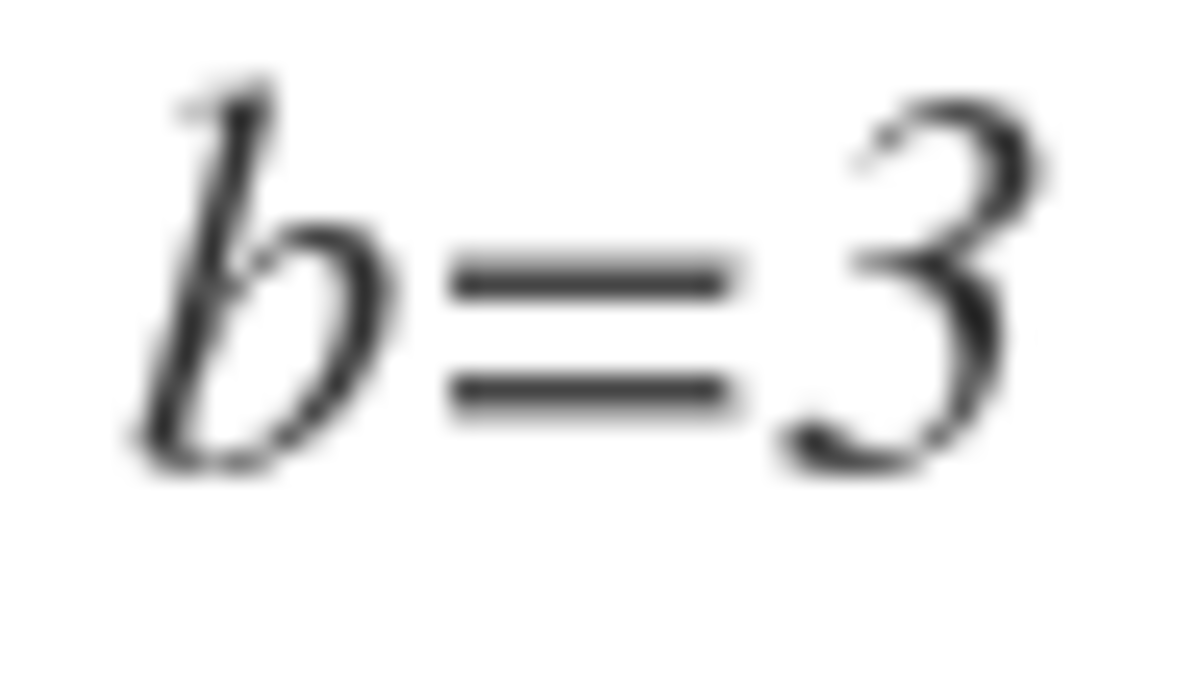 so
so
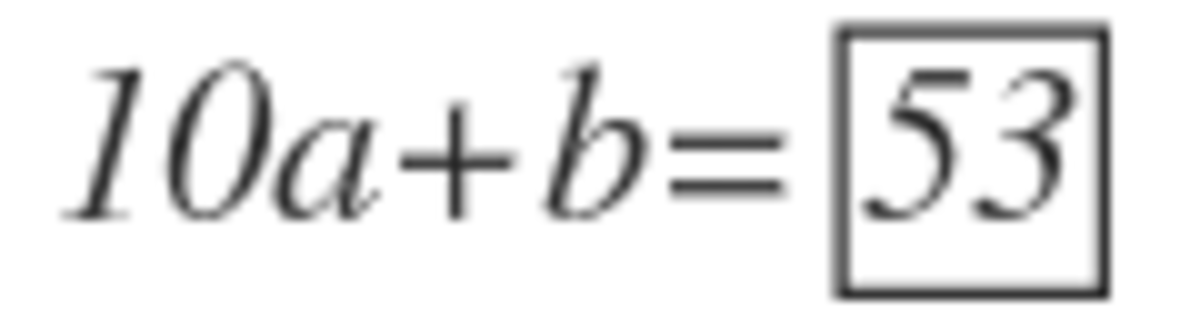
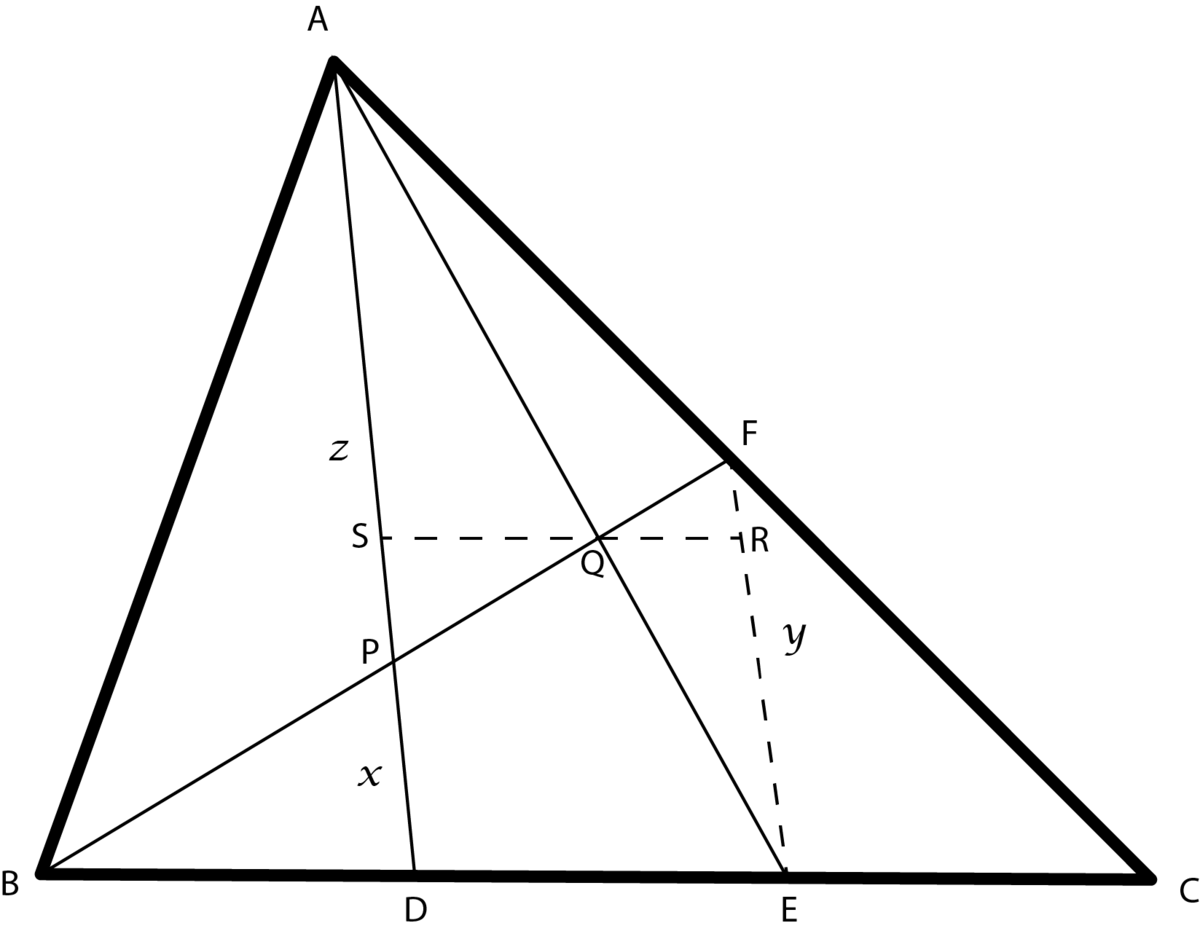
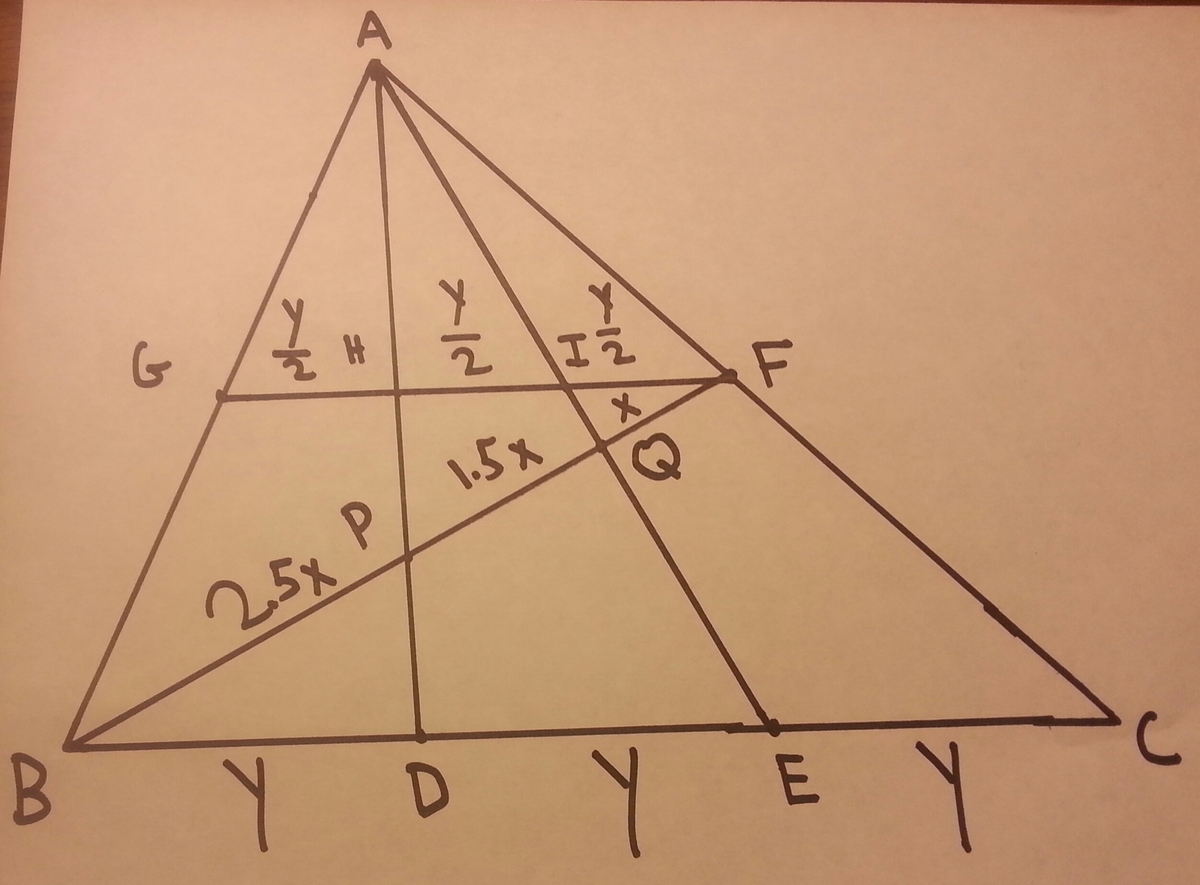
Contruction 1 . 2 . Join F E Draw S R ∥ B C
Let,
P D E F A P = x = y = z
Since
B D y x = D E , = 2 x = 2 y
∥ ly , z + x ⇒ z ⇒ Q P F Q = 2 y = 2 3 y = z y = 3 2
Now,
B P ⇒ B P ⇒ b a ⇒ a = 5 = P Q + Q F = ( 3 2 + 1 ) P Q = P Q B P = 3 5 b = 3
∴ 1 0 a + b = 5 3
Moderator note:
Interesting approach constructing those lines and points. What was the motivation for that?
Interesting approach constructing those lines and points. What was the motivation for that?
Log in to reply
I thought for almost a full day and finally assumed some similarity, which made me happy that I got the answer finally. But after a little thought I understood that it was wrong and further kept on visualizing triangle which were similar making me reach this method! Hence the run behind similar triangles is the motivation.
Construct D I and E J parallel to B F with I and J on A C .
Since, B D = D E = E C . It implies that F I = I J = J C . So, F J : F C = 2 : 3 . But since A F = F C . So, A F : F J = 3 : 2 .
Observe that, A Q : Q E = A F : F J = 3 : 2 .
Now let us do another construction. Draw a line parallel to A D passing through Q and meeting B C at Z .
Observe that D Z : Z E = A Q : Q E = 3 : 2 .
So, B D : D Z = D E : D Z = D Z + Z E : D Z = 3 2 + 1 = 5 : 3 .
But, it is clear that B P : P Q = B D : D Z = 5 : 3 .
So, a = 5 and b = 3 . Therefore, 1 0 a + b = 5 3 .