What name shall I give to this problem?
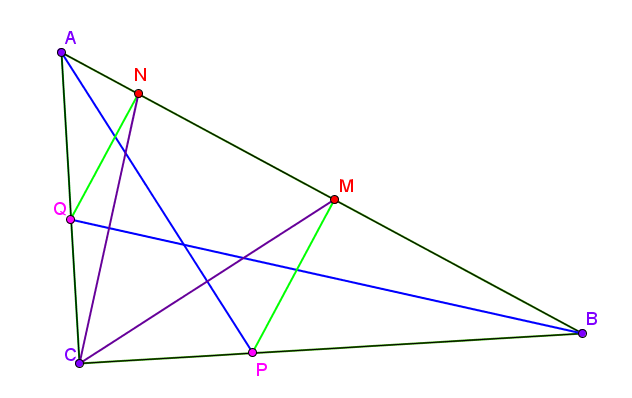 Let
be a right angled triangle with
. Suppose that
and
be the angular bisectors of
and
respectively. Let
and
be perpendiculars respectively from
and
on to
. Find the value of
(in degree).
Let
be a right angled triangle with
. Suppose that
and
be the angular bisectors of
and
respectively. Let
and
be perpendiculars respectively from
and
on to
. Find the value of
(in degree).
This problem is from the set What name should I give?
The answer is 45.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Observe that ∠ P M A + ∠ P C A = 1 8 0 o . So, P , C , A and M are cyclic. This implies that ∠ M C P = ∠ M A P .
Similarly, ∠ N C Q = ∠ N B Q .
So, ∠ M C N = 9 0 o − ∠ B C M − ∠ A C N = 9 0 o − ∠ A B Q − ∠ B A P = 9 0 o − 2 1 ∠ B A C − 2 1 ∠ C B A = 9 0 o − 2 1 ( ∠ B A C + ∠ C B A )
But, ∠ B A C + ∠ C B A = 9 0 o . So,
∠ M C N = 4 5 o