What Point Is This?

Geometry Level 3

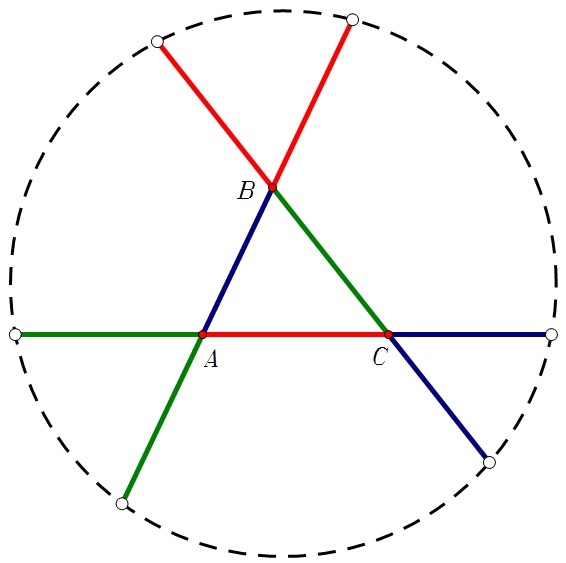
Let $ABC$ be any triangle, prolong the sides so that segments of the same color have the same length.

It can be shown that the six exterior points belong to the same circle $\Gamma$ [Try to prove this fact!]. Then complete the following sentence:

The center of $\Gamma$ is the $\ldots \ldots \ldots$ of triangle $ABC$ .

circumcenter orthocenter incenter barycenter

8 solutions

Avatar Anon
Jan 22, 2014

Each extended side contains a red section, a green section and a blue section. Thus, each extended side is equal in length. Each extended side is a chord of the circle and since chords of equal lengths are equidistant from the center of the circle, the point which is equidistant from the sides in a triangle is its incenter.

The concyclic nature of these 6 points can be proven using the converse of the power of a point (or intersecting chords) theorem: If segments $AB, CD$ intersect at point $E$ and $AE * EB = CE * ED$ , then $A, B, C, D$ lie on a common circle.

Michael Tong - 7 years, 4 months ago

very good solution!

Eloy Machado - 7 years, 3 months ago

Cleaner than mine, which proves that the necessary perpendicular bisectors are concurrent.

faraz masroor - 7 years, 3 months ago

Maharnab Mitra
Jan 22, 2014

I uploaded the image but it's not coming. So I again uploaded the image here. If you like it, please vote my "blank solution" above. If you like, you may vote this comment as well!

image

Maharnab Mitra - 7 years, 4 months ago

To prove the fact that they all lie on the same circle, use the converse of the power of a point theorem. If two segments, AB and CD, intersect each other at E, and AE * EB = CE * ED, then A, B, C, D lie on a common circle.

Michael Tong - 7 years, 4 months ago

Petko Petkov
Jan 22, 2014

The 3 heights of each isosceles triangle lie on the straight lines defined by each bisector of ABC so they intersect in the incenter of ABC. It's also the center of the big circle because each such straight line is perpendicular to the base of each isosceles triangle which is a chord in the big circle.

Nice argument!

Eloy Machado - 7 years, 3 months ago

Taehyung Kim
Jan 27, 2014

Noticing that the three chords of the circle are of the same length, we can conclude that these chords are equidistant from the center. Thus, by definition, this is the incenter.

Vaibhav Agarwal
Feb 23, 2014

Let us first name the points. B',B",C',C",A' and A" in the clockwise direction starting from the red line. We notice that B"AC' and A"AA' are similar (SAS) and thus angle AA"A'=AA'A"=AB"C'=AC'B"=x(say) Similarly, BB"B'=BB'B"=C"A'B=A'C"B=y(say) and CC'C"=CC"C'=CB'A"=A"B'C=z(say) and angle B=180 - 2y C= 180 - 2z and A=180-2x therefore, x+y+z=180 thus, B"C'C"A' CYCLIC (SUM OF OPPOSITES 180), C'C"A'A" CYCLIC (same reason) and A"A'B"B' cyclic (same reason). Therefore, all three points are cyclic Now, the centre will be the intersection point of the three lines which will pass through A""A', B"B', and C"C'...which willl all bisect the angles in front of them and thus meet at the incentre of ABC. Hence answer is incentre

Sauvik Mondal
Feb 11, 2014

using power of a point theorem,we see the 6 exterior points are concyclic.now green lines coomon to A forms an isosceles triangle(suppose its AMN)so perpendicular bisector of MN passes through A as well as centre of circle.but this perpendicular bisector also bisects angle A.so the centre is incentre of triangle

Michael Mendrin
Feb 3, 2014

Draw incircle of ABC. Then each of the lines are all of equal lengths, all at the same distance from the center of the incircle. Thus, they are all equal chords having the same apothem, which is true for any set of equal length chords in any circle.

Chandrasekhar Ch
Jan 23, 2014

As two outer edges at an angle of the triangle are of same length the angular bisector always passes through the center of the circle that is also the angular bisector of corresponding opposite angle of the triangle ABC, so the center of the circle becomes the intersection point of the angular bisectors i.e in-center. ( the angular bisector of an angle formed by two equal sides is always perpendicular to the other side of the triangle so it is diameter of the circle in this case.)

What Point Is This?

8 solutions

0 pending reports