What's the Radius?
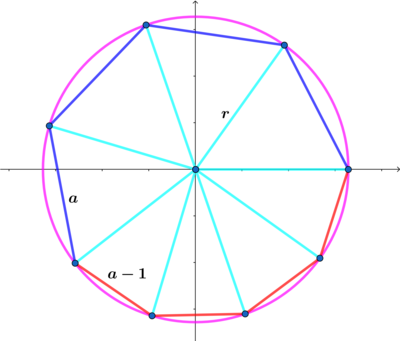
In the above diagram, the inscribed octagon has four consecutive sides of length a and four consecutive sides of length a − 1 .
If the area of the octagon is 1 3 + 1 2 2 , then the radius of the circle is r = β − λ ω α , where α , β , λ , and ω are coprime positive integers, find α + β + λ + ω .
The answer is 137.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
You can also write r = ( 2 6 − 1 2 2 ) ( 2 6 + 1 2 2 ) 9 7 ( 2 6 + 1 2 2 ) = 3 8 8 9 7 ( 2 6 + 1 2 2 ) = 2 1 3 + 6 2 , which seems a little easier.
Log in to reply
I didn't think of rationalizing the denominator. It's a nice simple form.
To find the value of a rearrange the octagon as shown above and inscribe it in a square.
Using the diagram above ⟹ 2 x 2 = ( a − 1 ) 2 ⟹ x − 2 a − 1
and the area of the square A s = ( a + 2 ( a − 1 ) ) 2 = ( ( 1 + 2 ) a − 2 ) 2 =
( 3 + 2 2 ) a 2 − 2 2 ( 1 + 2 ) a + 2
and
The area of the four right triangles is A T = 4 ( 2 1 ) 2 ( a − 1 ) 2 = ( a − 1 ) 2
The area of the octagon is
A c = A s − A T = ( 3 + 2 2 ) a 2 − 2 2 ( 1 + 2 ) a + 2 − ( a 2 − 2 a + 1 ) = 1 3 + 1 2 2
2 ( 1 + 2 ) a 2 − 2 ( 1 + 2 ) a − 1 2 ( 1 + 2 ) = 0 ⟹
a 2 − a − 6 = 0 ⟹ ( a − 3 ) ( a + 2 ) = 0 and a ≥ 0 ⟹ a = 3 ⟹ a − 1 = 2 .
Now to find the radius r of the circle:
Using the diagram above we have:
4 θ + 4 β = 3 6 0 ∘ ⟹ θ + β = 9 0 ∘ ⟹ β = 9 0 ∘ = θ
and
Using law of cosines ⟹ 9 = 2 r 2 ( 1 − cos ( θ ) ) and 4 = 2 r 2 ( 1 − cos ( β ) ) =
2 r 2 ( 1 − sin ( θ ) ) ⟹ 2 r 2 = 1 − sin ( θ ) 4 = 1 − cos ( θ ) 9
4 − 4 cos ( θ ) = 9 − 9 sin ( θ ) ⟹ 5 + 4 cos ( θ ) = 9 sin ( θ ) ⟹
( 5 + 4 cos ( θ ) ) 2 = 8 1 sin 2 ( θ ) = 8 1 − 8 1 cos 2 ( θ ) ⟹
9 7 cos 2 ( θ ) + 4 0 cos ( θ ) − 5 6 = 0 ⟹ cos ( θ ) = 9 7 − 2 0 ± 5 4 2
( 0 < θ < 9 0 ∘ ) ⟹ cos ( θ ) > 0 ⟹ cos ( θ ) = 9 7 − 2 0 + 5 4 2
⟹ r = 2 ( 1 − cos ( θ ) ) 3 and using the above value of cos ( θ ) ⟹
r = 2 6 − 1 2 2 9 7 = β − λ ω α
⟹ α + β + λ + ω = 1 3 7 .