A sliding rope!
In the figure shown, a uniform mass rope of length 5 m is released from rest. Find the velocity of the rope as it falls as a function of x .
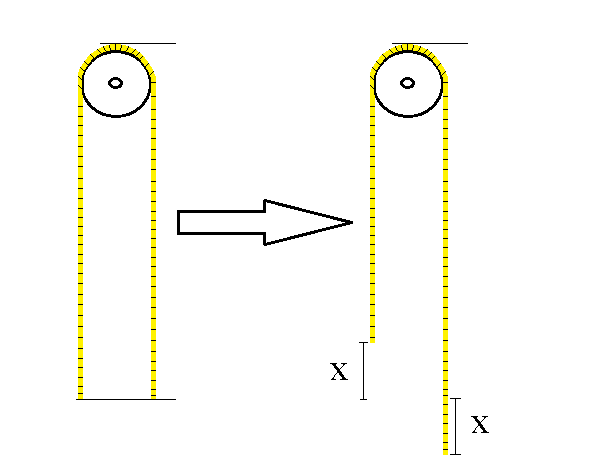
- Assume no length of rope around the pulley, i. e. rope much longer than pulley dimensions.
- g = 1 0 m / s 2
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Good one, but as this question is from Newton's Laws chapter, could you do it withou using energy? ;) (Yep, it is possible.)
Log in to reply
I bet it is possible. Perhaps you can post that solution.
To work this question around, you must consider this is a normal Atwood system. That said, we must write the Second Law for each sides of the rope. F n e t 1 = T − m 1 g F n e t 2 = m 2 g − T = m 1 a = m 2 a Where the first equation represents the right side of the rope (going up), and the second one represents the left side. Now to solve it, we need to find a relationship between m 1 and m 2 . It should be noted that, as the rope slides, m 1 and m 2 change in time.
Considering the fact that the rope is uniform we can assume that μ = 2 L M Where M is the mass of the rope, and 2 L is the length, in this case, 5 m .
Now, we have: I ) m 1 ( t ) I I ) m 2 ( t ) = μ ( L − x ) = μ ( L + x )
Solving the Newton Laws by Adding up: → → → → → I ) + I I ) : ( m 2 − m 1 ) g = ( m 1 + m 2 ) a → [ μ ( L + x ) − μ ( L − x ) ] g = [ μ ( L + x ) + μ ( L − x ) ] a → 2 μ x g = 2 μ L a → a = L x g → Rewriting $a$ as d x v d v d x v d v = L x g → v d v = x d x ( L g ) → ∫ 0 v v d v = ( L g ) ∫ 0 x x d x → v 2 = L g x 2 → v = x L g If you didn't understood step 7, be sure to checkout Velocity as a derivative here at Brilliant.
Consider the change in gravitational potential energy of the system. We can think of a length of rope x being taken from the left and transferred to the right (starting with the initial configuration).
The position of the rope segment's center of mass is originally + 2 x , and is − 2 x after being transferred. The overall change in height of the segment's center of mass is therefore − x .
The mass of the segment is L x M , where L is the total length and M is the total mass.
The decrease in gravitational potential energy relative to the start position is:
Δ U = L x M g x = L M g x 2
Equate the change in gravitational potential energy to the kinetic energy:
L M g x 2 = 2 1 M v 2 v 2 = L 2 g x 2 = 5 2 ( 1 0 ) x 2 = 4 x 2 ⟹ v = 2 x