What type of Quadric is this ? (2)
A quadric is given by,
r T A r + b T r + c = 0
where r = [ x , y , z ] T , and
A = ⎣ ⎡ 3 4 − 3 5 − 3 2 6 1 5 5 1 5 1 0 ⎦ ⎤
b = [ − 1 5 6 − 3 9 8 − 2 7 0 ] T
and
c = 1 8 2 6
What does the above equation represent graphically ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Very nice, Mark, I'd like to learn more about these techniques. I am not sure if we found the same line. Could you please check?
Log in to reply
Since r = P ⎝ ⎛ 1 0 1 1 4 2 7 λ ⎠ ⎞ = ⎝ ⎜ ⎛ 3 5 7 8 + 3 5 1 λ 3 5 1 9 9 + 3 5 3 λ 7 2 7 − 3 5 5 λ ⎠ ⎟ ⎞ = ⎝ ⎛ 3 − μ 8 − 3 μ 5 μ ⎠ ⎞ where μ = 3 5 2 7 − 3 5 1 λ , your and my line are the same.
Thanks very much!
Because of the way that Wolfram Mathematica works, some of the transpose operations had to be dropped in my solution.
r = { x , y , z } , a = ⎝ ⎛ 3 4 − 3 5 − 3 2 6 1 5 5 1 5 1 0 ⎠ ⎞ , b = { − 1 5 6 , − 3 9 8 , − 2 7 0 } , c = 1 8 2 6
Solve [ r . a . r + b . r + c = 0 , z ] ⇒ { { z → 1 0 1 ( − 3 5 − 9 x 2 + 6 x y + 6 x − y 2 − 2 y − 1 − 5 x − 1 5 y + 1 3 5 ) } , { z → 1 0 1 ( 3 5 − 9 x 2 + 6 x y + 6 x − y 2 − 2 y − 1 − 5 x − 1 5 y + 1 3 5 ) } }
Solve [ − 9 x 2 + 6 x y + 6 x − y 2 − 2 y − 1 ≥ 0 ] ⇒ { y → ConditionalExpression [ 3 x − 1 , x ∈ R ]
Fully simplified, with 3 x − 1 substituted for y in the solution for the original equation (above), yields { − 5 ( x − 3 ) , − 5 ( x − 3 ) } .
ParametricPlot3D [ { x , 3 x − 1 , − 5 ( x − 3 ) } , { x , − 2 0 , 2 0 } , BoxRatios → { 1 , 1 , 1 } , AxesOrigin → { 0 , 0 , 0 } ]
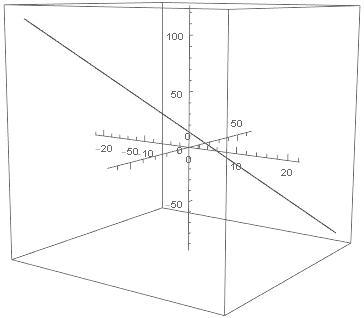
What is the difference between a pair of intersecting planes and a straight line so far as their 3-D equations are concerned?
I did not see two planes intersecting. I did see complex conics with only a straight line as real. That is why I selected a straight line. It is true that the intersection of two non-parallel planes is a straight line. The solution for the intersection of two non-parallel planes and of a straight line in three dimensions have the same form.
Evaluating r T A r + b T r + c gives the quadric equation: 3 4 x 2 + 2 6 y 2 + 1 0 z 2 − 6 x y + 1 0 x z + 3 0 y z − 1 5 6 x − 3 9 8 y − 2 7 0 z + 1 8 2 6 = 0
Setting y = z = 0 , I found no intersections with the x-axis.
Also, no intersection with y-axis or z-axis.
For the plane intersections below I used Excel to get it in standard form, performing a rotation and a translation of the coordinate systems. And I used it to convert solution coordinates back.
Intersection with yz-plane (x=0) is a single point: ( 0 , − 1 , 1 5 ) .
Intersection with xz-plane (y=0) is a single point: ( 3 1 , 0 , 3 4 0 ) .
Intersection with xy-plane (z=0) is a single point: ( 3 , 8 , 0 ) .
Intersection with plane x=1 is a single point: ( 1 , 2 , 1 0 ) .
Intersection with plane y=1 is a single point:: ( 3 2 , 1 , 3 3 5 ) .
For all planes I chose, I got a single point, and all points found were on the line parametrized by ( x , y , z ) = ( 3 − t , 8 − 3 t , 5 t )
As a check, putting these values for x, y, and z in the equation above gives 3 4 ( 3 − t ) 2 + 2 6 ( 8 − 3 t ) 2 + 1 0 ( 5 t ) 2 − 6 ( 3 − t ) ( 8 − 3 t ) + 1 0 ( 3 − t ) 5 t + 3 0 ( 8 − 3 t ) 5 t − 1 5 6 ( 3 − t ) − 3 9 8 ( 8 − 3 t ) − 2 7 0 ( 5 t ) + 1 8 2 6 = 0 which is just the identity.
The orthogonal matrix P = ⎝ ⎜ ⎛ 1 0 3 − 1 0 1 0 1 4 1 1 4 3 1 4 2 3 5 1 3 5 3 − 3 5 5 ⎠ ⎟ ⎞ is such that P T A P = ⎝ ⎛ 3 5 0 0 0 3 5 0 0 0 0 ⎠ ⎞ and hence the equation of the quadric becomes 3 5 X 2 + 3 5 Y 2 + α X + β Y + γ Z + c = 0 where ⎝ ⎛ X Y Z ⎠ ⎞ = P T r ⎝ ⎛ α β γ ⎠ ⎞ = P T b We calculate that α = − 7 1 0 , β = − 1 3 5 1 4 , γ = 0 , and so the equation of the quadric is 3 5 X 2 + 3 5 Y 2 − 7 1 0 X − 1 3 5 1 4 Y + 1 8 2 6 3 5 ( X − 1 0 1 ) 2 + 3 5 ( Y − 1 4 2 7 ) 2 = 0 = 0 and so the quadric is the straight line determined by the formulae X = 1 0 1 , Y = 1 4 2 7 , or the vector equation r = P ⎝ ⎛ 1 0 1 1 4 2 7 λ ⎠ ⎞ λ ∈ R