What's going on again?

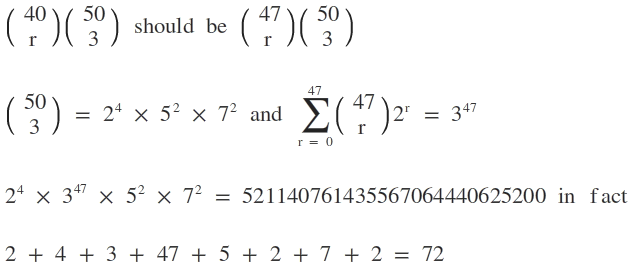
Consider the group of $50$ members.First select $r$ members from them. Give them red hats. From the remaining $50-r$ members, select $3$ members and give them blue hats. Let us provide cricket bats among red hat members for those who are willing to take. (It is not mandatory for everyone to take cricket bat.)

So, the number of possibilities for the above situation is ${50 \choose r} {50-r \choose 3} 2^{r}$ .

But the above situation is same even if we first select the three members from $50$ members and give them blue hats. Next from remaining $47$ members select $r$ members and provide cricket bats among these red hat members only for those who are willing to take.

So, summing up all the possibilities for all the value from $r=0$ to $r=47$ .

But this sum represents the number of possibilities of below situation.

1. Select $3$ members from $50$ members and them blue hats.

2. Among remaining $47$ members each person has three possibilities:- He is not eligible to take red hat.

• He is eligible to take red hat but not willing take the cricket bat.

• He is eligible to take red hat and willing to take the cricket bat.

So, from above the above situation, the total number of possibilities are

$\Large{{50 \choose 3} 3^{47}}$ $=2^{4} \times 3^{47} \times 5^{2} \times 7^{2}$ So, $a+b+c+d+e+f+g+h = \Large{\boxed{72}}$

Note ${50\choose r}{50-r\choose 3}2^r=\frac{50!(50-r)!}{(50-r)!r!(47-r)!3!}=\frac{50!}{r!(47-r)!3!}={40\choose r}{50\choose 3}$ .

Therefore,

$\displaystyle\sum_{r=0}^{47}{50\choose r}{50-r\choose 3}2^r={50\choose 3}\sum_{r=0}^{47}{47\choose r}2^r=50\cdot 49\cdot 8\cdot 3^{47}$

$\displaystyle=2^4\cdot 5^2\cdot 7^2\cdot 3^{47}$ , so the answer is $2+5+7+3+4+2+2+47=\boxed{72}$ .