What's that angle?
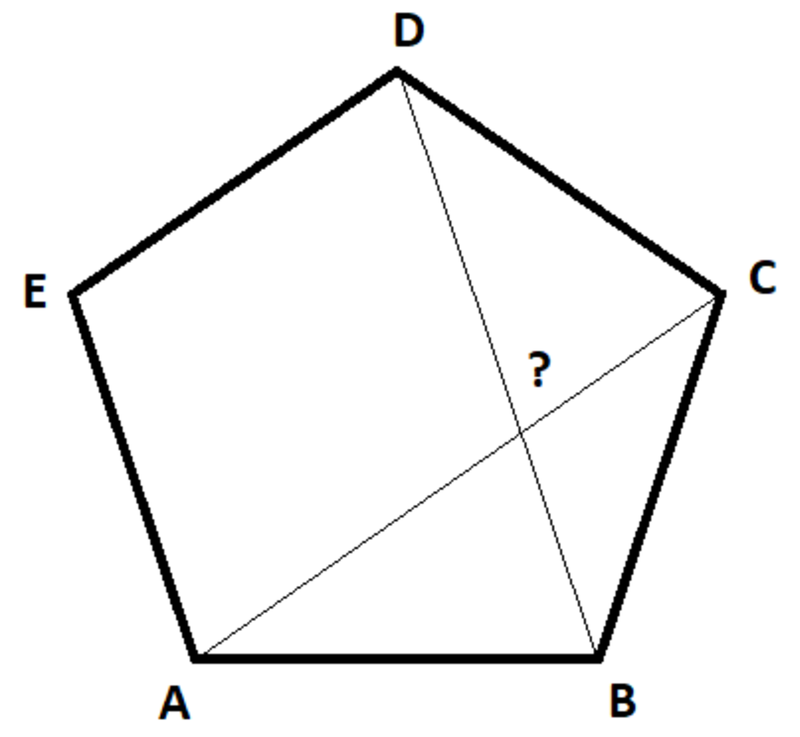
A B C D E is a regular pentagon. Find the measure of the angle (in degrees) between A C and B D .
The answer is 72.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
Add: "Since tri. DCB and tri. ABC are equilateral triangles we can see that: "
B D is a rotation of A C by an angle of 5 3 6 0 ∘ = 7 2 ∘ , so this is the angle between the two line segments.
You should add on the statement that we're looking for the acute angle (even though it's visible on the picture)
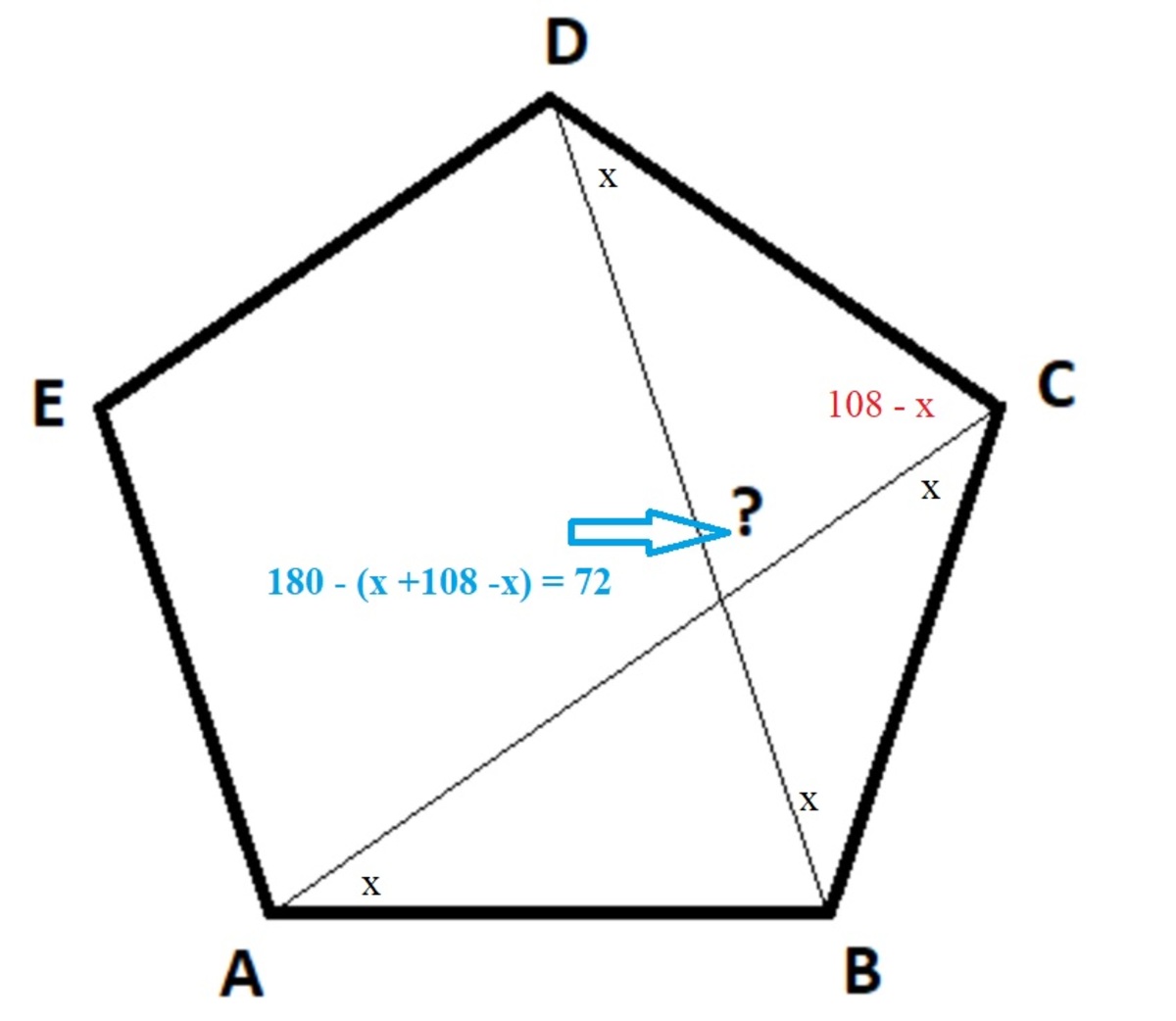
You guys can do 1) Si=( n-3) * 180 and divide the result for 2 . so Si=540° where n= the number of sides of the figure that is 5.
2) the figure has equal sides so the diagonal makes 2 oposite angules that has the same value in the figures that appers as a parallelogram. So if we know 1 angle is 108° and the other angle near to the ? angle is 108° we also can conclude that 108° + ?° will give us 180 because the sum of an internal angle with the external angle is equal to 180°
3) then 108 + ?°= 180 ?°= 180-108 ?°=72
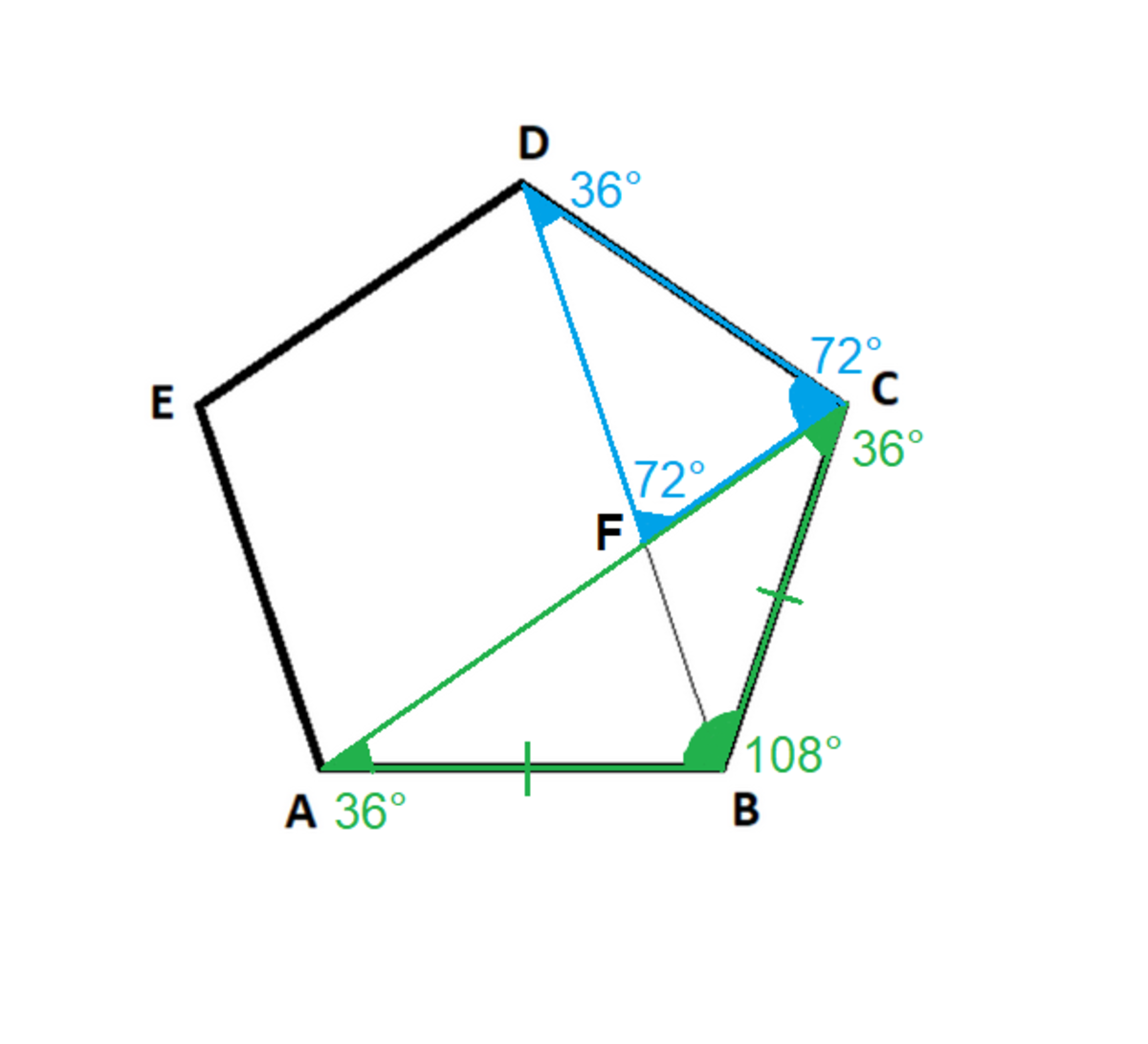 In a pentagon all angles add up to 540°. In a regular pentagon this means each of the 5 angles is 540°/5=108°. So angle A= angle B= angle C= angle D= angle E=108°.
In a pentagon all angles add up to 540°. In a regular pentagon this means each of the 5 angles is 540°/5=108°. So angle A= angle B= angle C= angle D= angle E=108°.
Since in a regular pentagon all sides are of equal length that means that AB=BC=CD=DE=EA. So triangle ABC is an isosceles triangle with equal sides AB and BC and a top corner B of 108°. In an isosceles triangle both base angles are the same, in triangle ABC that means that angle A=angle C= 2 1 8 0 ° − 1 0 8 ° =36°.
If we then look at triangle CDF we can see that we have an angle C of 108°-36°=72°. Angle D is the same angle as angle C in triangle ABC so angle D=36°. Angle F the angle we're looking for, then must be 180°-72°-36°=72°.
Is angle E is 108 degree and AEDF (F is that intersection point) is parallelogram so angleE=angleF now by linear theor. Required angle would be 180-108= 72.
In isosceles △ B C D we see ∠ D B C = ∠ B D C so it's clear that ∠ E D B = ∠ A B D , by similarity of △ F D C and △ F A B , ∠ E D B = ∠ A B D = ∠ A C D , an angle in a regular pentagon is 1 0 8 = ∠ E D B + ∠ B D C = ∠ A C D + ∠ B D C , so in △ B C D , ∠ ? = 1 8 0 − 1 0 8 = 7 2 .
Suppose the angle x. Observing the pantagon we can get the equation 180 - (x/2)*3 = 108 - 2/x . Solving this equation we get x = 72.
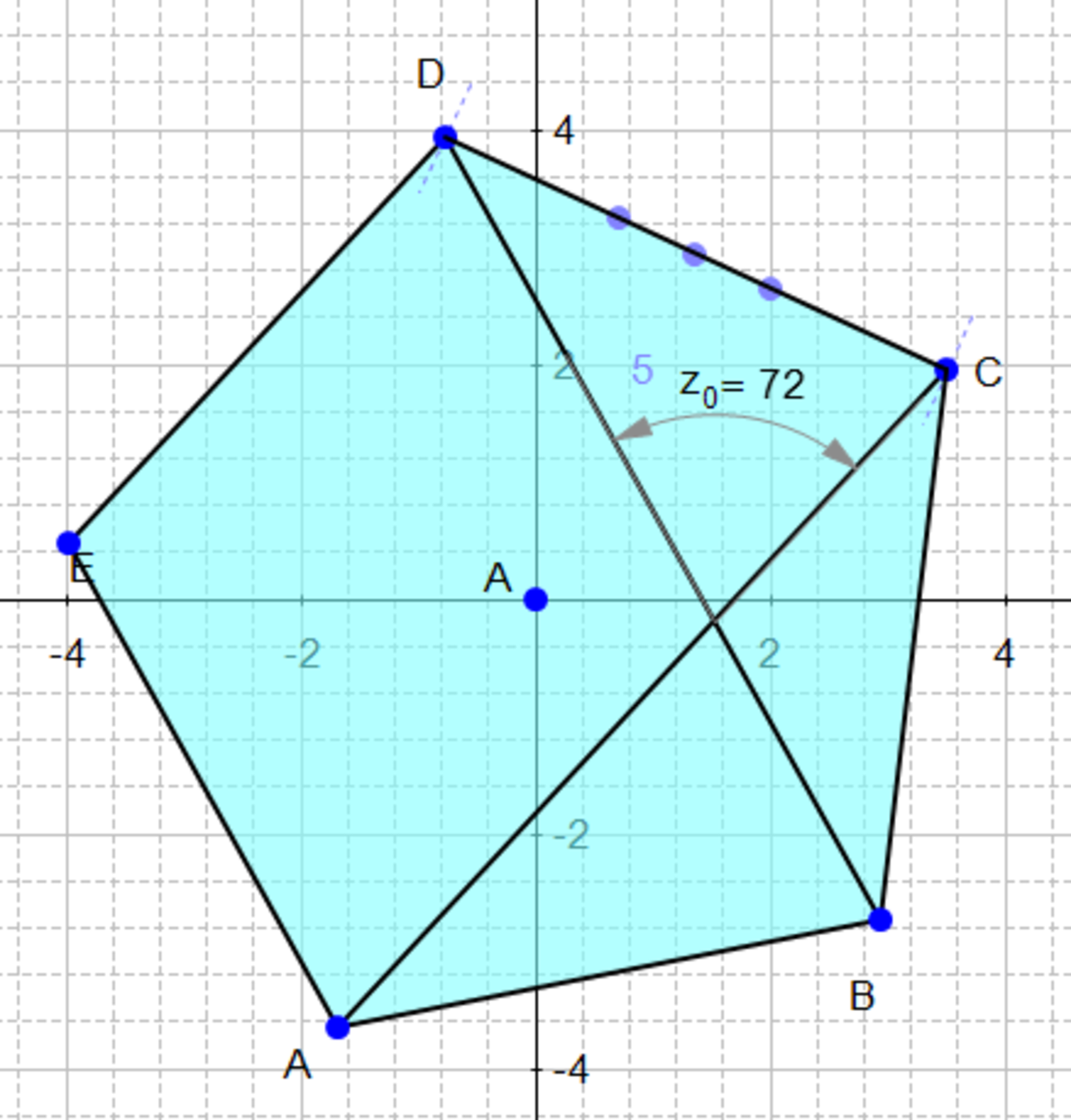
The colored dots indicate angles of equal measure. Due to symmetry △ B C F is isosceles and is similar to △ A D E . Therefore ∠ B F C = ∠ A E D = 1 0 8 ∘ and ∠ C F D = 1 8 0 ∘ − 1 0 8 ∘ = 7 2 ∘ .