What's that time?
Consider a clock with only minute hand and hour hand Take a close look at clock in Figure 1 The time is 4:00 If we interchange the position of hands we get the new time as shown in clock in Figure 2
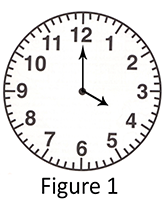
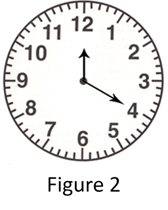
But this combination of hands ( Figure 2 ) cannot be achieved by usual tick-tock of clock because hour hand is exactly towards 12 and minute hand is towards 4 denoting 20 minutes. Consider all the times in a clock in 12 hours with the property that if we interchange the position of hands , the new position of hands i.e. new time does also exist.The time 12:00 is an example of this. Let be number of times with this propery in a clock in 12 hours.
Between and with , and denoting hours in clock ( is for 12) , let the time with that property be with denoting minutes.
Then can be expressed as : with , , and are integers and and are co-prime.
Find where denotes floor function.
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let H : M be the time with that property between H and H + 1 where 0 ≤ H ≤ 1 1 , H ∈ Z and M ∈ R
We know that in 1 minute, minute hand rotate through 6 ∘ and hour hand rotate through 2 1 ∘ .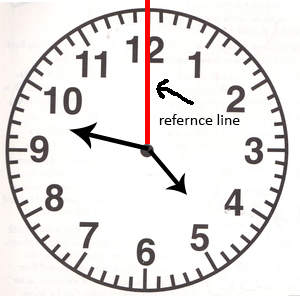
So, the angular position of minute hand with respect to reference line (line joining centre to 12) in clockwise direction will be 6 M ∘ and that of hour hand in clockwise direction will be 3 0 H ∘ + 2 M ∘ .
Let after interchanging the hands, the time be H R : M R here also H R and M R are defined as H and M .
Now, the minute hand will be at the angular position of 3 0 H ∘ + 2 M ∘ and hour hand will be at the angular position of 6 M ∘
i.e. 6 M R ∘ = 3 0 H ∘ + 2 M ∘ ⋯ E q . 1 and 3 0 H R ∘ + 2 M R ∘ = 6 M ∘ ⋯ E q . 2
Using Eq. 1 in Eq. 2 ,
3 0 H R ∘ = 6 M ∘ − 2 6 3 0 H ∘ + 2 M ∘
⇒ 3 0 H R = 2 4 1 4 3 M − 2 5 H ⋯ E q . 3
But H R is a integers, so, H R is greatest integer less than or equal to 3 0 ∘ 6 M ∘ ⇒ H R = ⌊ 3 0 ∘ 6 M ∘ ⌋ ⋯ E q . 4
Using Eq. 4 in Eq. 3
3 0 ⌊ 3 0 ∘ 6 M ∘ ⌋ = 2 4 1 4 3 M − 2 5 H ⇒ 2 4 1 4 3 M = 2 5 H + 3 0 n
where n = ⌊ 3 0 6 M ⌋ = ⌊ 5 M ⌋ N o w , 0 ≤ M < 6 0 ⇒ 0 ≤ 5 M < 1 2 ⇒ 0 ≤ ⌊ 5 M ⌋ ≤ 1 1 ⇒ 0 ≤ n ≤ 1 1 , n ∈ Z
⇒ M = 1 4 3 2 4 × ( 2 5 H + 3 0 n )
⇒ M = 1 4 3 6 0 ( H + 1 2 n )
So the time with that property in between H and H + 1 is
H : 1 4 3 6 0 ( H + 1 2 n ) , 0 ≤ n ≤ 1 1
We see that for every permissible value of H there are 1 2 values of n and so 1 2 values of M . And there are 12 possible values of H form 0 to 1 1 . So in 12 hours there are 1 2 × 1 2 = 1 4 4 times possible with that property. But in counting time 12 :00 is counted 2 times , one by taking H = n = 11 and other by taking H = n = 0.
Hence there are 144 - 1 = 143 times possible . ⇒ m = 1 4 3
Comparing the calculated expression of M with c a ( H + b n ) we get
a = 6 0 , b = 1 2 , c = 1 4 3
⌊ b c ⌋ − ⌊ a m ⌋ = ⌊ 1 2 1 4 3 ⌋ − ⌊ 6 0 1 4 3 ⌋ = 3