What's the acceleration?
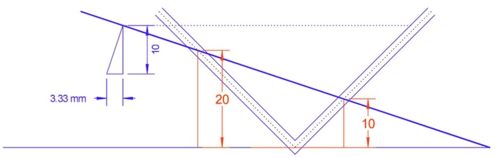
An accelerometer is made using tubular sections, as shown below. The accelerometer is placed in a rocket that travels in the x direction, and the liquid levels are steady at 2 0 c m and 1 0 c m .
Find the magnitude of the rocket’s acceleration (in m/s 2 ). Submit your answer to 3 decimal places.
Details and Assumptions:
- The diameter of the tube is much smaller than the heights of the liquid in the two arms.
- g = 1 0 m/s 2 .
The answer is 3.333.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
Nice solution! What is the physics reason for the water surface being perpendicular to the combined acceleration?
Log in to reply
Any liquid settles so its surface is perpendicular to the force being applied to it, eg. the surface of a lake responding to gravity. From the perspective of the liquid, there's only one force of acceleration acting on the system. And since we know that g makes up the y component of the force on this liquid, we can calculate the x component, which corresponds to the rocket's acceleration, using vector addition.
Log in to reply
Nice incisive explanation Kyle. The whole thing becomes relateable and intuitive if you turn the picture so the force only consist of a y component. Also, the illustration is slightly misleading, because the surface of the water on both sides would in reality have the same slope as the "fall" from the first side to the second.
Still i am not able to understand .
The problem is awkward because it forces us to make assumptions that cannot be justified. The solution above is correct IF the rocket is traveling (and accelerating) parallel to the surface of a planet where g=10 m/s^2. Perhaps I should have read "rocket" as "car driving along smooth linear highway". Also, Jacob's line is perhaps more significant than the illustrator of the problem may have noticed. His line shows an approximation of the true surface shape that the water would take under the 2 assumed influences (gravity and rocket), discounting a meniscus.
Log in to reply
Yes, I cleared that up in another comment with the following quote: "the illustration is slightly misleading, because the surface of the water on both sides would in reality have the same slope as the "fall" from the first side to the second."
Could this problem be done by considering the free body diagrams for left column and right column separately? The forces would be force due to the pressure by the other column, gravity and net force due to the pressure exerted by the container. I seem to get the same answer by solving the 4 equations that I get from 2 FBDs.
Log in to reply
Yes, that will work too. You just have to be a bit careful about forces where the two columns meet.
Log in to reply
Can we not assume that there is some pressure at the bottom of the tube, and that pressure is omni-directional? That is, the force due to the pressure will act on any surface in the normal direction.
Interestingly, the pressure at the bottom is neither proportional to10g nor 20g (plus atmospheric pressure).
As per the illustration above, this problem can be solved geometrically:
- The water is in equilibrium, therefore the force on it must be perpendicular to the water level, and it is shown as r .
- g is the force of gravity, of length 10 per definition
- Therefore a is the force due to the acceleration of the rocket
- Because the slant of vector r is 3 (goes up three units for each unit going right), a is 10 / 3 = 3.3333.
Nicely explained solution. Upvoted!
Denote the mass of the fluid as 3 m . Consider the force and acceleration along the tube since the fluid cannot move perpendicular to the tube. Then the net force along the tube is m g cos 4 5 ∘ . The sum of the force along the tube equals the mass times the acceleration along the tube:
m g sin ( 4 5 ∘ ) = 3 m a cos ( 4 5 ∘ )
Therefore a = 3 g
actually it is 3macos(theta) = mgsin(theta). Theta is 45 and sin(45) = cos(45) so it cancels
The tube is not straight. It has two different directions, so how did you find the force along the tube?
just treat it like any other force and pretend the tube is straight
Easiest to do this graphically with vectors. Water always seeks its lowest point; therefore the magnitude of acceleration must be such that the water "thinks" that the 20cm/10cm distribution is level. The rear water level is 10 cm higher than the front one, and 30 cm to the rear. A line connecting the two water levels "feels" to the water like a level surface. The acceleration vector must be perpendicular to this line, so it must extend downward and to the rear with the same ratio of 3:1. The downward component of the acceleration is g (10 m/s), so the (fictitious) rear-ward acceleration experienced by water must be 10/3.
It is fascinating that water seeks its lowest point; its surface is always perpendicular to the "effective" gravity. Do you know why this happens?
Resolve the two acceleration vectors (g and a) into components down the tubes and perpendicular to the tubes. The left tube has a "down the tube" acceleration of (g - a)/sqrt(2) and the right hand side has a "down the tube" acceleration of (g + a)/sqrt(2).
Pressure at bottom from left tube = Pressure at bottom of right tube
=> (density) x (tube length L) x (area) x "down tube acceleration L" / (area) = (density) x (tube length R) x (area) x "down tube acceleration R" / (area)
=> (density) x (20/sqrt(2)) x A x (10 - a)/(sqrt(2)) x 1/A = = (density) x (10/sqrt(2)) x A x (10 + a)/(sqrt(2) ) x 1/A
=> (20) x (10 - a) = (10) x (10 + a), thus a = 10/3
I'm not sure if this solution is correct but I got the right answer:
Assuming no force other than gravity was acting on the water, the height of each side would have to be equal. In order to keep the same volume while doing this, both sides would end up being 15 cm in height. The force x brings it down by 5, which is 1/3 of 15. 1/3 of the gravitational constant, 10, is 3.3333 m/s^2. Therefore, x has to be 3.3333 m/s^2
You have got the right answer, but the reasoning can be better explained.
If there was no other force than gravity, then both sides will have the same level. However, the tube is accelerated rightwards, which causes a horizontal force on the system. In the ground frame, we say that there is a "fictitious" force opposite to direction of acceleration. This is the force which pushes the water level in the right side down and the left side up.
The key point is that the pressure at both the water surfaces is same and equal to atmospheric pressure. Using equations of pressure (pressure increases linearly with depth), the acceleration can be found.
If you consider a slightly different setup, you will see that the answer will depend on the difference in water levels, and the distance
d
as well.

Could you explain how you found the acceleration using your diagram? Thanks!
Great diagram! Why do liquids maintain a horizontal with respect to effective gravity?
Reference from the topic Rigid body motion under fluid mechanics of Mechanical engineering: When a fluid mass in a container is subjected to a motion such that there is no relative motion between the particles, such a motion is known as rigid body motion. The motion can be either translation or rotation at constant acceleration or a combination of both. As in the given question it has mentioned only about translation so I am using the concept of fluid dynamics, the fluid is under pure translation with a uniform acceleration the piezometric head will have a gradient in the direction of motion. Motion is in x direction with a constant acceleration a(x), then:
-(dh/dx) = tan θ = {a(x)/g}
dh = differential height or difference in height
dx = distance covered or difference between two points in a x-direction
θ = angle
a(x) = acceleration in x-direction
g = gravity
Could you explain how you got the equation tan θ = g a ?
Log in to reply
You might have seen full equation -(dh/dx) = tan θ = {a(x)/g}, a is horizontal to the surface and g is perpendicular to surface. While the fluid is in motion, fluid from front limb gets displaced and shifts. Now join free surface of fluid in both limbs you'll get a triangle. Then you apply the concept of geometry and you'll get the result tan θ= {a(x)/g}. For reference some people have solved it and have a look at their diagrams too. Thank you.
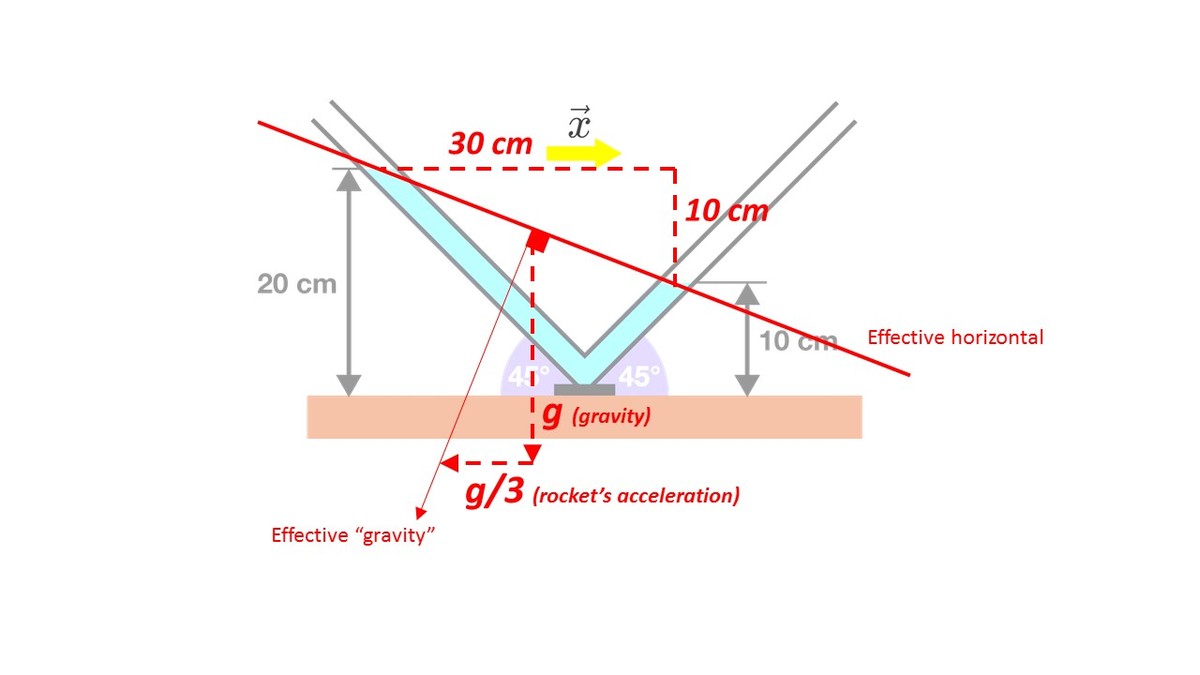
First, we realise that the combined acceleration (g + rocket) must be perpendicular to a drawn line between the surface of each side of the water. Now, we also realise that the slope of this line compared to g must in fact represent the exact acceleration necessary applied from the rocket to maintain mentioned position of the water.
We calculate the slope as follows: 3 0 c m ( 1 0 c m − 2 0 c m ) = − 3 1 (since the accelerometer is set at a 45 degree angle, this one should be fairly obvious)
Meaning that in order to change the angle of force to match our new setup, we have to apply a horizontal force that is 3 1 of the vertical one (g).
Consider this beautiful illustration: (Remember, the accelerations are perpendicular to what the triangle displays, hence g is horizontally drawn)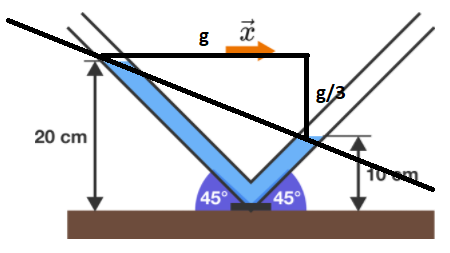 Conclusively, the answer is
3
g
=
3
.
3
3
.
.
.
s
2
m
Conclusively, the answer is
3
g
=
3
.
3
3
.
.
.
s
2
m
Sorry if this was confusing, done late hours.