What's the Area of the Region?
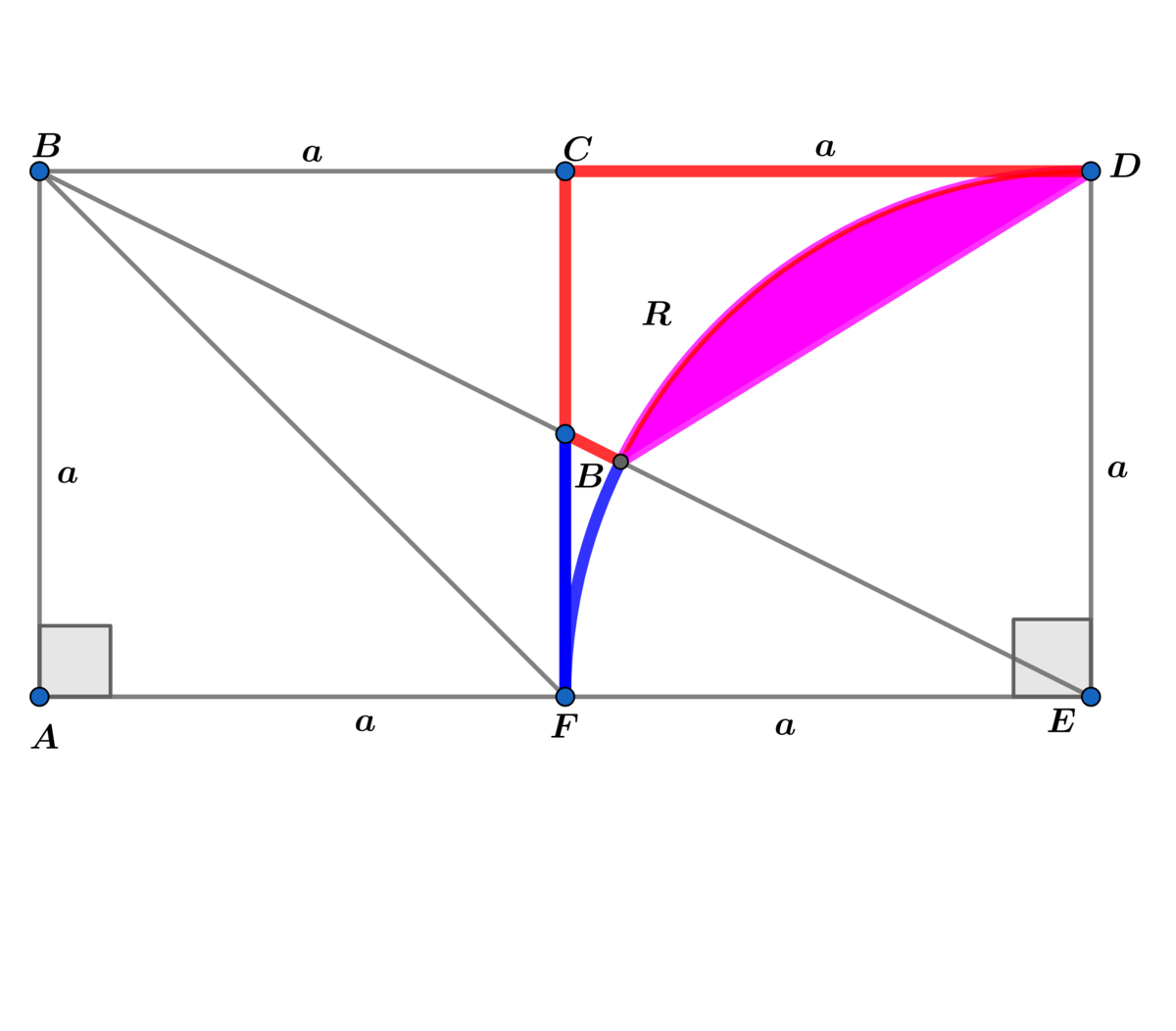
In the diagram above the two regions are labeled R and B .
If the area of the pink region A P = 2 1 and A R = β β α ( α arctan ( β ) − β ω − β arctan ( β ) ) , where α , β ω are coprime positive integers, find α + β + ω .
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
By the Pythagorean Theorem on △ B D E , B E = B D 2 + D E 2 = ( 2 a ) 2 + a 2 = 5 a , so tan ∠ B E D = a 2 a = 2 and sin ∠ B E D = 5 a 2 a = 5 2 .
The area of the sector formed by E B D is A sec E B D = 2 π m ∠ B E D π a 2 = 2 1 a 2 arctan ( 2 ) .
The area of △ E B D is A △ E B D = 2 1 a 2 sin ∠ B E D = 5 1 a 2 .
Then A p = A sec E B D − A △ E B D = 2 1 a 2 arctan ( 2 ) − 5 1 a 2 = 2 1 , which solves to a 2 = 5 arctan ( 2 ) − 2 5 .
And A R = A F C D E − A △ F B E − A sec E B D = a 2 − 4 1 a 2 − 2 1 a 2 arctan ( 2 ) = 4 3 − 2 arctan ( 2 ) ⋅ 5 arctan ( 2 ) − 2 5 = 2 2 5 ( 5 arctan ( 2 ) − 2 3 − 2 arctan ( 2 ) ) .
Therefore, α = 5 , β = 2 , ω = 3 , and α + β + ω = 1 0 .
△ A B E ∼ △ F M E ⟹ 1 2 = F M a ⟹ F M = 2 a ⟹ A △ F M E = 4 a 2
and tan ( θ ) = 2 1 ⟹ θ = arctan ( 2 1 ) ⟹ A s e c t o r ( F P E ) = 2 1 arctan ( 2 1 ) a 2 ⟹
A B = A △ F M E − A s e c t o r ( F P E ) = ( 4 1 − 2 1 arctan ( 2 1 ) ) a 2 ⟹
A R = a 2 − 4 π a 2 − A B = ( 4 3 + 2 1 arctan ( 2 1 ) − 4 π ) a 2
To Find a 2 using A P = 2 1 :
B E = 5 and tan ( λ ) = tan ( 2 π − θ ) = tan ( θ ) 1 = 2 ⟹
A s e c t o r ( P D E ) = 2 1 arctan ( 2 ) a 2 and h = a sin ( λ ) = a cos ( θ ) = 5 2 a ⟹
A △ P D E = 2 1 ( a ) ( 5 2 a ) = 5 a 2 ⟹ A P = 2 1 = A s e c t o r ( P D E ) − A △ P D E =
( 2 5 5 arctan ( 2 ) − 2 ) a 2 ⟹ a 2 = 5 arctan ( 2 ) − 2 5
Using the fact that θ = arctan ( 2 1 ) and λ = 2 π − θ = arctan ( 2 ) ⟹
θ = 2 π − arctan ( 2 ) ⟹ A R = 4 5 ( 5 arctan ( 2 ) − 2 3 − 2 arctan ( 2 ) ) =
β β α ( α arctan ( β ) − β ω − β arctan ( β ) ) ⟹ α + β + ω = 1 0 .