What's the Area of the Region ?
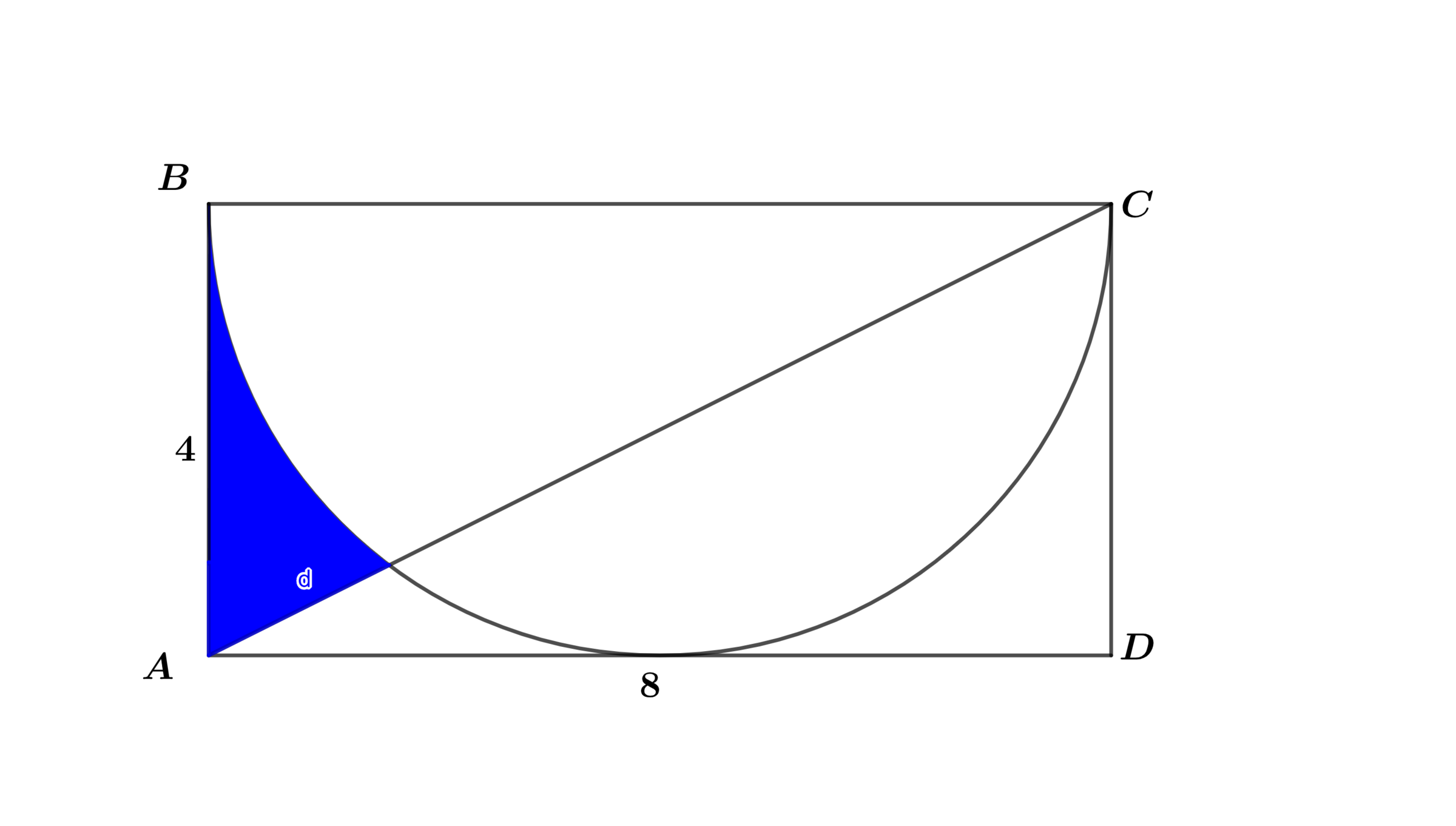
If the area of the shaded region in Rectangle above with diagonal and inscribed semicircle whose diameter is can be represented as
, where and are coprime positive integers, find .
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Using the diagram above the equation of line A C is y = 2 1 x or x = 2 y and for the circle centered at (4,4) with have ( x − 4 ) 2 + ( y − 4 ) 2 = 1 6
x = 2 y ⟹ ( 2 y − 4 ) 2 + ( y − 4 ) 2 = 1 6 ⟹ 5 y 2 − 2 4 y + 1 6 = 0 ⟹
y = 5 4 , y = 4 Since we already have ( 8 , 4 ) ⟹ P ( 5 8 , 5 4 )
So the area of the pink region is A 1 = 2 1 ( 5 4 ) ( 5 8 ) = 2 5 1 6 .
( x − 4 ) 2 + ( y − 4 ) 2 = 1 6 ⟹ x = 4 − 1 6 − ( y − 4 ) 2 which is the portion of the circle needed.
The area of the blue region is A 2 = ∫ 5 4 4 ( 4 − 1 6 − ( y − 4 ) 2 ) d y
For I = ∫ 1 6 − ( y − 4 ) 2 d x
Let y − 4 = 4 sin ( θ ) ⟹ d y = 4 cos ( θ ) ⟹ I = 8 ∫ ( 1 + cos ( 2 θ ) ) d θ
= 8 ( θ + sin ( θ ) cos ( θ ) ) = 8 ( arcsin ( 4 y − 4 ) + 1 6 ( y − 4 ) 1 6 − ( y − 4 ) 2 )
⟹ ∫ 5 4 4 ( 1 6 − ( y − 4 ) 2 ) d y = 8 arcsin ( 5 4 ) + 2 5 9 6
⟹ A 2 = 5 6 4 − 2 5 9 6 − 8 arcsin ( 5 4 ) = 2 5 2 2 4 − 8 arcsin ( 5 4 )
∴ The total area A ∗ = A 1 + A 2 = 5 4 8 − 8 arcsin ( 5 4 ) = 8 ( 6 / 5 − arcsin ( 5 4 ) ) = 2 3 ( 5 2 ∗ 3 − arcsin ( 5 2 2 ) ) = a b ( c a ∗ b − arcsin ( c a a ) ) .
Note: For A 2 you could have used:
A 2 = ∫ 0 5 8 ( 4 − 1 6 − ( x − 4 ) 2 − 5 4 ) d x = ∫ 0 5 8 ( 5 1 6 − 1 6 − ( x − 4 ) 2 ) d x