What's the area of the right triangle!

Geometry Level pending

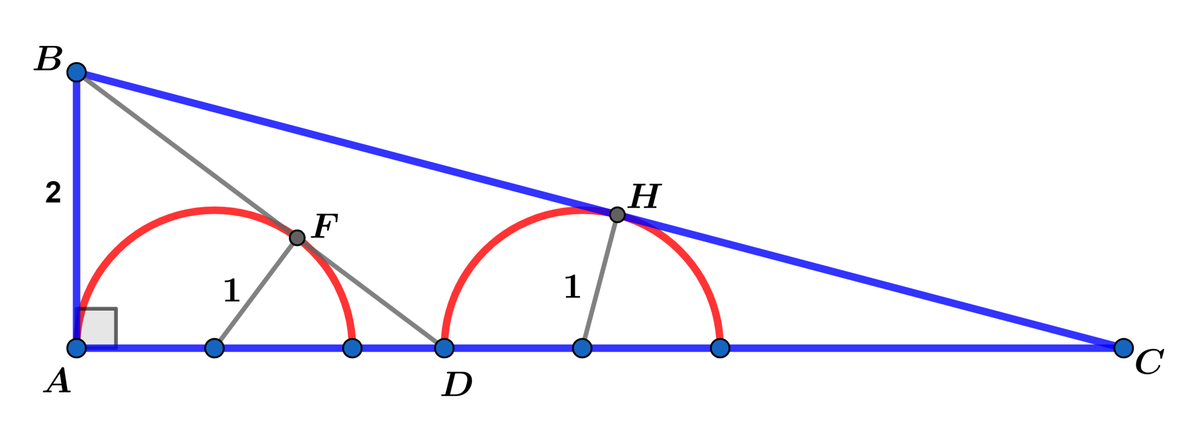
In right $\triangle{ABC}$ with $\overline{AB} = 2$ , $\overline{BD}$ and $\overline{BC}$ are tangent to the two inscribed semicircles with radius 1 at $F$ and $H$ respectively.

If $A_{\triangle{ABC}}= \dfrac{a(b + \sqrt{c})}{d}$ , where $a,b,c$ and $d$ are coprime positive integers, find $a + b + c + d$ .

The answer is 61.

2 solutions

Rocco Dalto
Mar 8, 2021

$\triangle{ABD} \sim \triangle{EFD} \implies \dfrac{2}{1} = \dfrac{\overline{BD}}{y} \implies \overline{BD} = 2y$

Using the Pythagorean theorem on $\triangle{ABD} \implies 4y^2 = 4 + (1 + y)^2 \implies$

$3y^2 - 2y - 5 = 0 \implies y = \dfrac{5}{3}$ dropping the negative root $\implies \overline{AD} = \dfrac{8}{3} \implies$

$\overline{AG} = \dfrac{11}{3}$

$\triangle{ABC} \sim \triangle{GHC} \implies \dfrac{2}{1} = \dfrac{\overline{BC}}{x} \implies \overline{BC} = 2x$

Using the Pythagorean theorem on $\triangle{ABC} \implies 4x^2 = 4 + (\dfrac{11}{3} + x)^2 \implies$

$36x^2 = 36 + 121 + 66x + 9x^2 \implies 27x^2 - 66x - 157 = 0 \implies x = \dfrac{11 + 4\sqrt{37}}{9}$

dropping the negative root $\implies \overline{AC} = \dfrac{11}{3} + \dfrac{11 + 4\sqrt{37}}{9} =$

$\dfrac{4(11 + \sqrt{37})}{9} \implies A_{\triangle{ABC}} = \dfrac{4(11 + \sqrt{37})}{9} = \dfrac{a(b + \sqrt{c})}{d}$

$\implies a + b + c + d = \boxed{61}$ .

What would happen if you kept extending the diagram? So, draw another unit semicircle through $C$ , construct the tangent from $B$ , mark the intersection with the extended line $AC$ , and so on. Is there a "nice" formula for the area after $n$ semicircles?

Chris Lewis - 3 months ago

I worked out the following below with Area $A_{1} = \dfrac{m^3}{m^2 - 1}$ , where $m$ is the height of right $\triangle{ABC}$ .

Let $d_{1} = \dfrac{2m^2}{m^2 - 1}$

and for $n \geq 1$ define:

$d_{n + 1} = \dfrac{m}{m^2 - 1}((d_{n} + 1)m + \sqrt{(d_{n} + 1)^2 + m^2 - 1})$ and $A_{n + 1} = \dfrac{m}{2}d_{n + 1}$ .

I'm going to post the problem as follows:

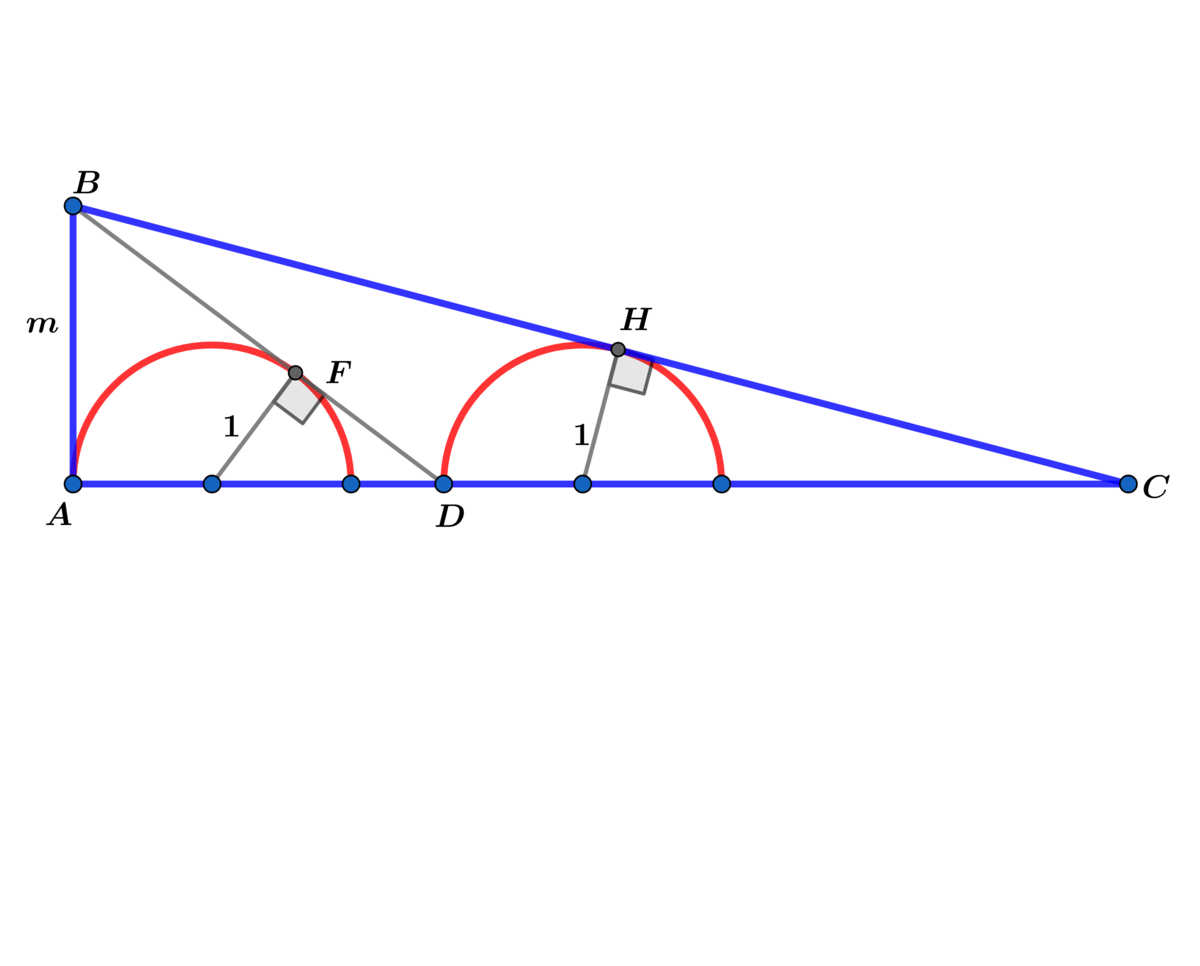
Let $m > 1$ .

In right $\triangle{ABC}$ with $\overline{AB} =m$ , $\overline{BD}$ and $\overline{BC}$ are tangent to the two inscribed unit semicircles at $F$ and $H$ respectively.

Extend the above diagram to $n$ congruent unit circles as follows:

Draw another unit semicircle through C and construct the tangent from B and mark the intersection with the extended line AC and continue this process for the $n$ unit semicircles.

(1) Find the a formula for the area of the right triangle formed which contains the $n$ unit semicircles.

(2) Using $m = 2$ and $n = 10$ write a program to compute the area of $A_{n}$ .

I arrived at $A_{10} = \boxed{2473.004638671875}$ .

Rocco Dalto - 3 months ago

Chew-Seong Cheong
Mar 10, 2021

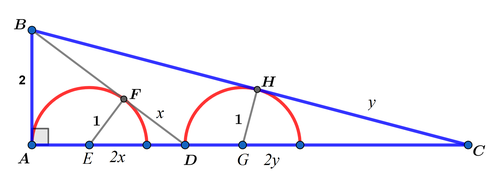
Let the centers of the left and right semicircle be $E$ and $G$ . Note that $\triangle DEF$ and $\triangle ABD$ are similar. If $FD = x$ , $AD = 2x$ . By Pythagorean theorem , we have:

$\begin{aligned} EF^2 + DF^2 = DE^2 = (AD-AE)^2 \\ 1^2 + x^2 & = (2x-1)^2 \\ 1 + x^2 & = 4x^2 - 4x + 1 \\ 3 x^2 & = 4x & \small \blue{\text{Since }x \ne 0} \\ 3x & = 4 \\ \implies x & = \frac 43 \\ AD & = 2x = \frac 83 \end{aligned}$

Similar, since $\triangle CHG$ and $\triangle ABC$ are similar. If $HC = y$ , $AC = 2y$ and

$\begin{aligned} HG^2 + CH^2 & = CG^2 = (AC-AD-DG)^2 \\ 1^2 + y^2 & = \left(2y- \frac 83 - 1 \right)^2 \\ 1 + y^2 & = 4y^2 - \frac {44}3y + \frac {121}9 \\ 27y^2 - 132y + 112 & = 0 \\ \implies y & = \frac {22+2\sqrt{37}}9 & \small \blue{\text{The small }y < 2} \end{aligned}$

Since $A_{triangle ABC} = \dfrac 12 \cdot AB \cdot AC = 2 y = \dfrac {4(11+\sqrt{37})}9$ . Therefore $a+b+c+d = 4 + 11 + 37 + 9 = \boxed{61}$ .

What's the area of the right triangle!

The answer is 61.

2 solutions

0 pending reports