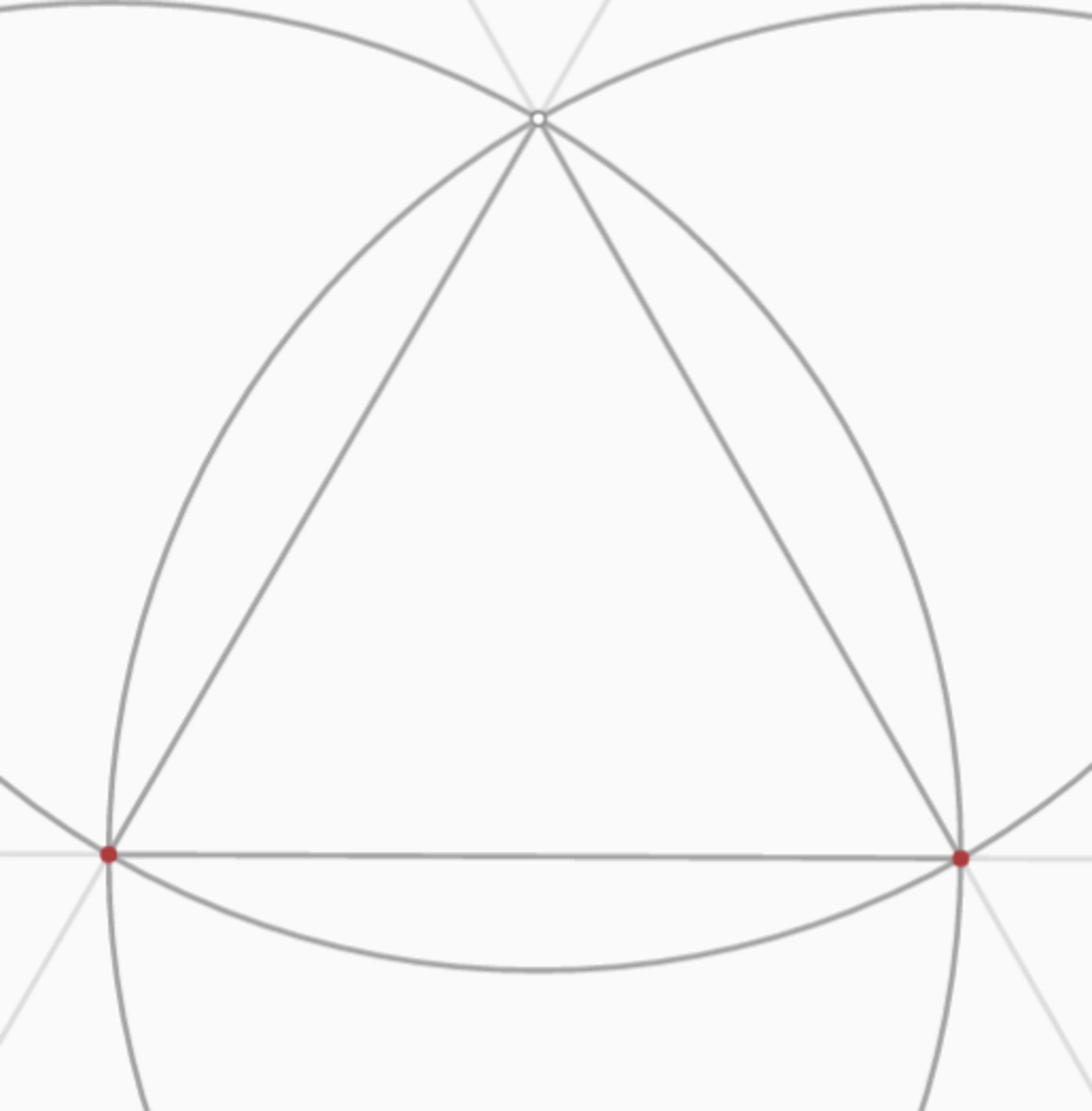
What's the area of this shape, -10? (I)

${\color{#20A900}{A_{\text{Reuleaux triangle}}}}= {\color{#D61F06}{3 \times A_{\text{segment}}}} + {\color{#3D99F6}{A_{\text{triangle}}}}$ . Each of the 3 minor segments is equal due to symmetry, hence their areas are equal. The area is equal to:

$\begin{aligned} {\color{#D61F06}{A_{\text{segment}}}} &= A_{\text{sector}} - A_{\text{triangle}} \\ &= \bigg(\dfrac{60}{360} \cdot \pi (7)^2 \bigg) - \bigg(\dfrac{\sqrt{3}}{4} \cdot (7)^2 \bigg) \\ &= (7)^2 \times \bigg(\dfrac{1}{6} \cdot \pi - \dfrac{\sqrt{3}}{4}\bigg) \\ \\ {\color{#3D99F6}{A_{\text{triangle}}}} &= \bigg( \dfrac{\sqrt{3}}{4} \cdot (7)^2\bigg) \end{aligned}$

---

$\begin{aligned} {\color{#20A900}{A_{\text{Reuleaux triangle}}}} &= {\color{#D61F06}{3 \times A_{\text{segment}}}} + {\color{#3D99F6}{A_{\text{triangle}}}} \\ &= {\color{#D61F06}{3 \times (7)^2 \times \bigg(\dfrac{1}{6} \cdot \pi - \dfrac{\sqrt{3}}{4}\bigg)}} + \color{#3D99F6}{\bigg( \dfrac{\sqrt{3}}{4} \cdot (7)^2\bigg)} \\ &= (7)^2 \times \bigg( \dfrac{1}{2} \pi - \dfrac{3\sqrt{3}}{4} + \dfrac{\sqrt{3}}{4}\bigg) \\ &= (7)^2 \times \bigg( \dfrac{1}{2} \pi - \dfrac{1}{2} \sqrt{3} \bigg) \\ &= \dfrac{1}{2} (7)^2 \big(\pi - \sqrt{3} \big) \\ {\color{#20A900}{A_{\text{Reuleaux triangle}}}} &\approx 35 \implies \text{Answer is 35 - 10} = \boxed{25} \end{aligned}$

We can see that instead of $7$ as the radius of the circle, we can generally let radius to be $r$ . Thus the formula will be: $\boxed{\dfrac{r^2}{2}\big(\pi - \sqrt{3} \big)}$

Area of the given shape is $3\times \left (\frac{1}{2}\times 7^2\times \frac{π}{3}-\triangle \right ) +\triangle$ , where $\triangle$ is the area of the equilateral triangle $=\frac{\sqrt 3}{4}\times 7^2$ .

That is, the required area is $\frac{49(π-\sqrt 3)}{2}\approx 34.533775$ or $35$ when rounded off.

The required answer is $35-10=\boxed {25}$ .

First we solve for the equilateral triangle's area.

$A = \frac{\sqrt{3}}{4}a^2$ (where $a$ is the side length of the triangle)

$A = \frac{\sqrt{3}}{4} × 49$

$A ≈ 21.21762$

By rounding off, we get:

$A ≈ 21$

Then, we find the area of the outer three circle chords by using the area of a sector of this circle

$\frac{60}{360} × \frac{22}{7} × 7 × 7$

$\frac{22 × 7}{6}$

$25\frac{2}{3}$

Subtracting from the triangle's area, we get:

$25\frac{2}{3} - 21 = 4\frac{2}{3}$

When multiplying by three to get the area of all the three chords, we get

$4\frac{2}{3} × 3 = \boxed{14}$

By addition to get the total area of the Reuleaux triangle, we get:

$21 + 14 = \boxed{35}$

According to the question, we should subtract the final value by $\boxed{10}$

$35 - 10 = \boxed{25}$