What's the area?

By medians propierties $CG=8$ and $BG=6$ ). Then is known that medians divides a triangle in six triangles of equal areas $\therefore$ area of $\triangle BGC =$ area of $\triangle AGC=$ area of $\triangle AGB$ ; as $\triangle BGC$ is right angle triangle with cathetus $6$ and $8$ its area is $\frac{6\times8}{2}=24 \Rightarrow$ the area of $\triangle ABC=24\times 3=\boxed{72}$

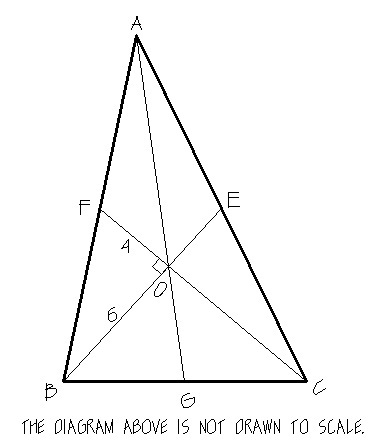
The three medians of a triangle meet in a point, the centroid, which is situated on each median so the measure of the segment from the vertex to the centroids is two-third the measure of the median. So

$FO=\dfrac{1}{3}(12)=4$

$BO=\dfrac{2}{3}(9)=6$

The three medians of a traingle divide the triangle into six equal areas, so the area of triangle $ABC$ is

$A_{ABC}=6\left(\dfrac{1}{2}\right)(6)(4)=$ $\boxed{72}$

We notice that quadrilateral FEBC is an orthogonal quadrilateral, so its area is the product of its diagonals divided by two, which is $\frac{9\cdot 12}{2}=54$ . We then see, since points F and E are midpoints, that line segment FE is a midline. Thus, triangle AFE is one fourth of the area of the whole triangle, and so quadrilateral FEBC is three fourths the area of the whole triangle. Therefore, our answer is $\frac{4}{3}\cdot 54=\boxed{72}$ .