What's The Biggest Box That Can Be Cut From This Cardboard?
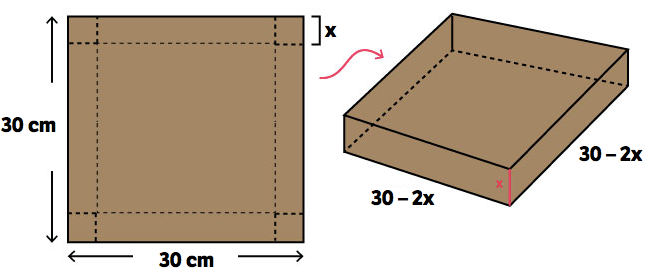 At Sandy's Candies, for a fixed price, you can purchase a square sheet of cardboard 30 cm by 30 cm. This cardboard can then be made into a box, by cutting equal squares from all four corners and folding up the flaps. You may then take as many chocolates as will fit in the box.
At Sandy's Candies, for a fixed price, you can purchase a square sheet of cardboard 30 cm by 30 cm. This cardboard can then be made into a box, by cutting equal squares from all four corners and folding up the flaps. You may then take as many chocolates as will fit in the box.
What is the side length (in cm) of the squares you should cut from the corners to make a box that will hold the most chocolates?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
21 solutions
The problem can be generalized. Consider a square of length L with square corners of length x cut out and the resulting sides folded up to form a box. For what value of x is the volume of the box maximum?
From the diagram of the problem statement:
V ( x ) = x ( L − 2 x ) ( L − 2 x )
Multiplying,
V ( x ) = 4 x 3 − 4 L x 2 + L 2 x
The domain of V is [ x ∣ 0 ≤ x ≤ 2 L ] = [ 0 , 2 L ] .
The significance of the endpoints is that they result in zero volume. x = 0 is not cutting the corners and folding the sides up, x = L/2 results in nothing or a point.
Taking the first derivative, setting it equal to zero and the second derivative, it is proven that V is maximum when x = 6 L .
The maximized volume of the box is V ( 6 L ) = 2 7 2 L 3
Function is x(30x-2x)^2 . Put derivative equal to zero, x=5 or 15, 15 isnt logical so hence 5 is the answer.
i think this problem is based on differentiation
Simple, 1cm=0.39Inch.. Substitute the four given options (Which is in CM) to (11-2x) or (8-2x) a) 0 is not valid- as it gives d same size.. b)15CM = 6IN.. It will go more beyond the actual size.. c)5CM = 1.9IN.. It gives reasonable ans.. d)10CM = if we cut, our ox will b small
Volume of a cuboid = L x B x H
since cardboard will be cut by x cm, Volume becomes: __(30 - 2x)(30 - 2x)(x)
which equals: Volume = 4(x^3) - 120(x^2) + 900x
We differentiate the above equation (USE THE CALCULUS APPLIED MAXIMA MINIMA CONCEPT IN THIS SCENARIO)
achieve: V ' = 12(x^2) - 240(x) + 900
Solving this quadratic, we achieve x = 15 or 5
Thinking logically, if we take 15cm as x, we are doing nothing but cutting the whole box's length and width out lol. So we automatically have the answer as x = 5 cm
I just eliminate 0 & 15 as answer before solving the question.
just think of it with simple logic
beautiful
nice...
V(x)= x(30-2x)(30-2x) V(x) = 4x^3-120x^2+ 900x V'(x) = 12x^2 - 240x + 900 , where V'(x) is = 0 0= 12x^2 - 240x + 900 by using quadratic equation: X1= 15, X2=5 Substituting in the eqn. V(x) = 4x^3-120x^2+ 900x V(15) = 4(15)^3-120(15)^2+ 900(15) V(15) = 0 V(5) = 4(5)^3-120(5)^2+ 900(5) V(5) = 2000 cm^3
Using a graphic will help prove better the reason why 5 is the correct answer. Because we have F(x)=y= box volume. From this,using the derivative just once will show in the graphic the points we have and will also show seamlessly that 5 is a max point.
x ( 2 0 − 2 x ) 2 = 4 1 [ 4 x ( 2 0 − 2 x ) ( 2 0 − 2 x ) ] ≤ 4 1 ( 3 4 x + 2 0 − 2 x + 2 0 − 2 x ) 3 = 2 0 0 0 from AM-GM.
x = 5 , 2 0 yields the maximum of 2 0 0 0 , but x = 2 0 is outside the feasible domain so the answer is 5 .
volume =(30-2x)(30-2x)x differentiate 30-2x= 4x x=5
A blind person can solve this !
There are four options 0, 5, 10, 15.
To cut 4 squares with the side length of 0 cm and 15 cm is nat possible.
If we cut out squares from the board having a side length of 5 cm and make a box with the cardboard, the volume of the board will be (30−2×5)×(30−2×5)×5=2000
And if we cut out squares from the board having a side length of 10 cm and make a box with the cardboard, the volume of the board will be (30−2×10)×(30−2×10)×10=1000
So, if we cut out squares from the board having a side length of 5 cm and make a box with the cardboard, the box will have the most volume and also can hold the most number of chocolates.
So, the answer is 5
d
it's very simple...for the box to get max chocolate it's volume should b maximum. if u take x = 1) 0 then its volume = 30x30x0 = 0 cm^3 2) 5 then volume = (30-2x5)x(30-2x5)x5 = 20x20x5 = 2000 cm^3 3) 10 then vol = (30-20)x(30-20)x10 = 10x10x10 = 1000cm^3 4) 15 then vol = 0 because no base area so correct ANS = 5 that it hope it helps.........:):):):)
when we cut equal squares of length 5cm then height of box=5cm width=length=20cm and in this way volume of box is maximum than all other cases so it will contain maximum chocolates :)
Four options: 0, 5, 10, 15. It's said that you NEED TO CUT somewhere near the corner to form a box. So, 0 is impossible because 0 means you don't cut anything.
Then, only 5, 10, 15 are left. Since we were asked the minimum value, then choose 5. HAHA.
THIS IS ONLY FOR MULTIPLE CHOICE. DON'T TRY THIS METHOD WHEN IT ISN'T.
(1)The expression for the volume of the box is x(30-2x)(30-2x). (2)Expand to give 4x^3-120x^2+900x. (3)Differentiate to give 12x^2-240x+900. (4)Make (3) equal to zero, to find the turning points, therefore the local maximum and local minimum of (2). (5)Divide through by 12 to get 0=x^2-20x+75. (6)Factorize and solve to give x=5, x=15. (7)Since (2) is a cubic with a positive x^3 term, the turning point with the lesser x value is the local maximum, or use d^2y/dy^2 to do it. (8)x=5.
TO FILL MOST CHOCOLATES THE VOLUME OF THE BOX SHOULD BE MAXI. LET THE VOLUME OF THE BOX IX V. THEN V=(30-2x)(30-2x)x [v=f(x)] then f'(x)=0 at x=5,15 and f''(x)=-ve at x=5 so x=5 Vix maximum.
0 &15 options are cancelled as if x=0 no cardboard will form and if x=15 the whole sheet is cutted into 4 equal squares
now if x=5 then area in which we have to keep chocolates is 400 square units and if x=10 then the area is 100 square units. so, if x=5 we will have max. area.
This problem is an example of an optimization problem which means that we have to get the absolute value that will be the value of the side of the corner in order for the box to hold the maximum no. of chocolates. If x is the length of the side of the squares to be cut out, the volume of the box will be: v(x)=(30-2x)(30-2x)(x) Thus, v'(x)=12x^2-240x+900 =12(x-5)(x-15) Note that x has to be less than half the width of the cardboard because v must be positive. this means that x must be included in (0, 15) and hence the only critical number is 5. Using the Second Derivative Test, v"(x)=24x-240 v"(5)=-120 v"(5)<0 Therefore, v has a relative maximum at x=5 and since it is the only relative extremum in the interval (0, 15), x=5 is also the absolute maximum on (0, 15).
Finally, we can conclude that the maximum length of the side of the square to be cut from the cardboard is 5 cm. so that it can hold the most number of chocolates.
Find V (Volume) in terms of x. Put dV/dx = 0 and solve for x. Get the values of second derivative. Observe that the second derivative is negative at x = -5. Accept x = -5. ignore sign.
sorry, we do get x = 5
I solved the problem by the method of calculus.
Volume of the box, V=(30-2x)^2*x
=4x^3-120x^2+900x.
The rate of variation of the volume, V with the variation of x can be expressed as
dV/dx=12x^2-240x+900
For the volume to be maximum or minimum, dV/dx=0
i.e 12x^2-240x+900=0
Solving the above equation we get x=15 or x=5
Viewing the figure itself, we see that V=0 when x=15
Thus, for the maximum value of V, x=5
This one is so simple. From the given options, the least no. will be the solution (since higher the magnitude higher will be its area) 0 is not possible, because we cannot make a box without cutting the edges. So, 5 is the best answer.
You have to take the first derivative of algebraic volume and equate to zero to find the value of x.
30x30=900 but we need the next greatest area so removing squares of 5cm each we get the area as 20x20=400
We have with ourselves a cardboad which has square dimensions and now we want to make it into box by cutting squares from the side. This box can be seen as a cuboid with a top open. So, we have to find the cuboid with maximum volume.
Differentiate the total volume to get the maxima and minima points - X x (30-2X) x (30-2X) , x=>5,0
The objective is to simply find such a value of x for which the volume of the box is maximum.Hence volume = l b h=x*(30-2x)^2. Now to get max. volume dV/dx = 0 . On solving you get x=5.
but if i did >> (cut 10cm each i’ll get the max volume (length20 width20 height10=4000))
We want to maximize the volume of the box, so we need to determine our formula for the volume this box. V ( x ) = ( x ) ( 3 0 − 2 x ) ( 3 0 − 2 x ) The height is x and the other two dimensions are 3 0 − 2 x since whatever we cut from one side needs to also be cut from the other one, as in the image. Now we find the derivative and find a root, which may be a maxima. V ′ ( x ) = 1 2 ( x 2 − 2 0 x + 7 5 ) = 1 2 ( x − 5 ) ( x − 1 5 ) x = 5 This may be proven if we notice that the second derivative if negative at x = 5 V ′ ′ ( x ) = x − 1 0 V ′ ′ ( 5 ) < 0