What's the difficulty?

The answer is none of the others. Or technically all of the others. The reason is that such triangle doesn't exist . In a right-angled triangle, the height to the hypotenuse cannot be more than half of the length of the hypotenuse. Computing naively gives the height of $2 \cdot \frac{12}{6} = 4$ , but this is more than half the length of the hypotenuse 6, so the triangle cannot exist.

To prove that the height to the hypotenuse cannot be more than half of the length of the hypotenuse, consider a circle with the hypotenuse as the diameter. The right-angled vertex must then lie on the circle. Thus, the height of the triangle cannot be greater than the radius of the circle, which is half of the hypotenuse.

(Technically, because the premise cannot be satisfied, the conclusion can be arbitrary. This is why I said "all of the others" is also valid; you can conclude anything from a contradiction. But I hope the point of the question is clear enough either way.)

What about a rigorous calculus solution? :)

Let the triangle be fixed into a semicircle.

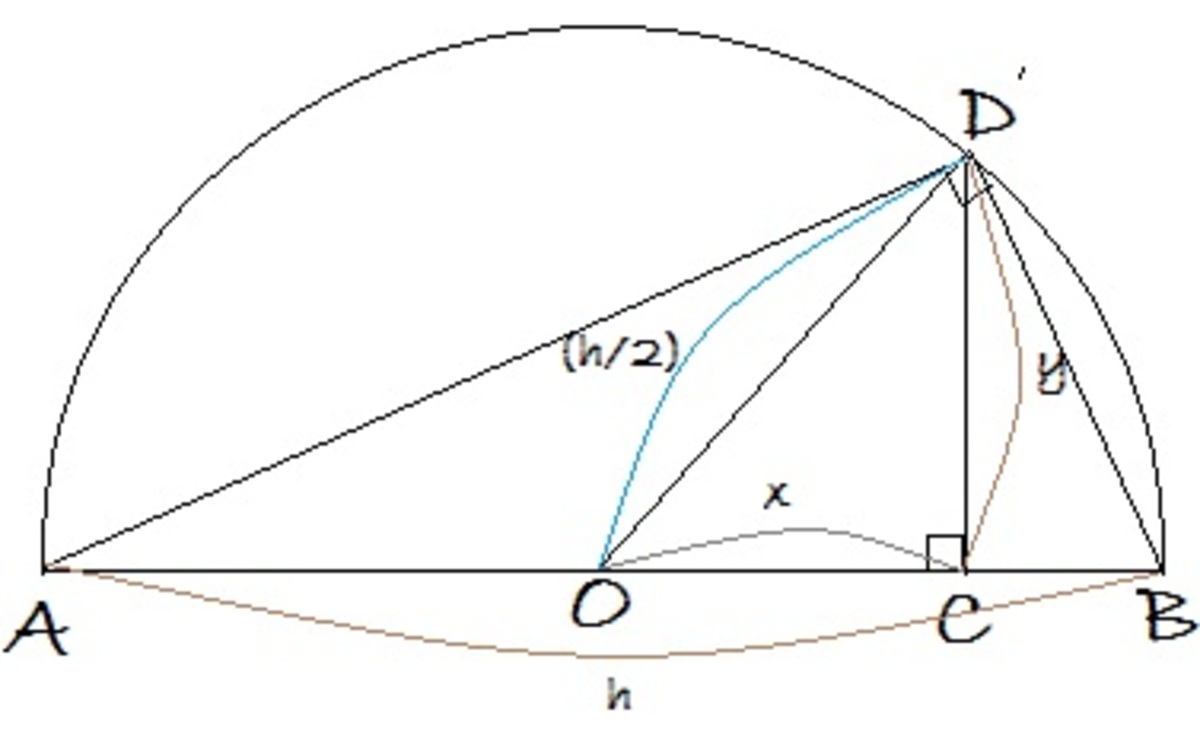
As shown, $AC$ is the triangle's hypotenuse as well as the semicircle's diameter. $D$ is a random point on the non-diametrical part of the circle. $OD$ is joined. Evidently, $OD$ is the radius and is half the hypotenuse length. Now $C$ is a point of the diameter $AB$ such that $CD ⊥ AB$ . Clearly, $DC$ is the perpendicular from the hypotenuse. $AC$ and $BD$ are joined. Now, moving our focus towards right triangle $OCD$ , we have to find the maximum value of $DC$ . Let $DC=y$ , $OC=x$ and $OD=(h/2)$ (where, $AB=h$ ). Now, applying Pythagorean Theorem in tr. $OCD$ , we have:

Since we have to find the extrema of y (if exists any, as such), we differentiate it with respect to x and equate it to 0. We find $\frac{dy}{dx}=0$ gives $x=0$ . Now substituting $x=0$ in $\frac{d^{2}y}{dx^{2}}$ evaluates to $\frac{-2}{h}$ , while we know that $h$ is the semicircle diameter and is positive. Clearly, $\frac{-2}{h}$ is negative and so is $\frac{d^{2}y}{dx^{2}}$ . We know that if we differentiate a function and equate its first derivative to $0$ and find the value of the parent variable and substitute it in its second derivative and it yields a negative value, then a maximum value of the function exists and is equal to the value of the function when its parent variable is equal to its value obtained while equating the first derivative to $0$ . Now relating to our case, we get $x=0$ from the first derivative. Hence substituting $x=0$ in the function leads $y=\frac{h}{2}$ , which is the maximum value of $y$ .

So, the maximum height of the perpendicular to the hypotenuse of a triangle is equal to half of the hypotenuse.

We find that the perpendicular to the hypotenuse is $4 cm$ and more than half of its hypotenuse $6 cm$ . Hence such a triangle doesn't exist.

I had posted a problem similar to this based on this relation between the hypotenuse length and length of the perpendicular of the hypotenuse. Well, that turned out to be a Level 2 question. :3

Let one of the legs of the triangle be $x$ , so the other leg is $\sqrt{36-x^2}$ . Observe that the altitude to the hypotenuse is 4. Then, we have the following equation.

$\sqrt{x^2-16}+\sqrt{36-x^2-16}=6$

This equation has no solution, so the answer is none of the above.