What's the height?
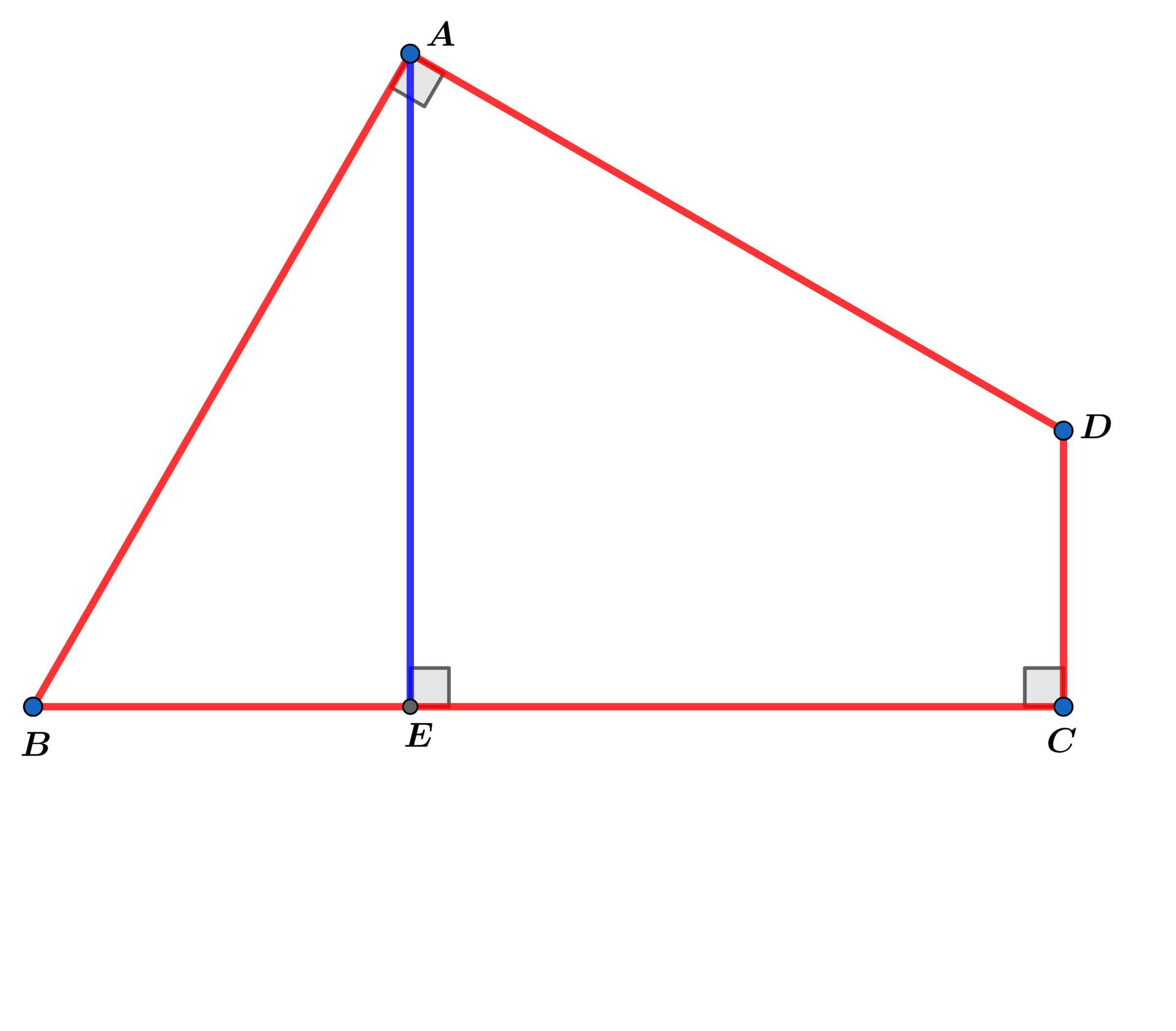
In quadrilateral A B C D , ∠ A , ∠ C and ∠ A E C are right angles and A B ≅ A D .
If the area A A B C D = 1 0 0 , find the height A E of quadrilateral A B C D .
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
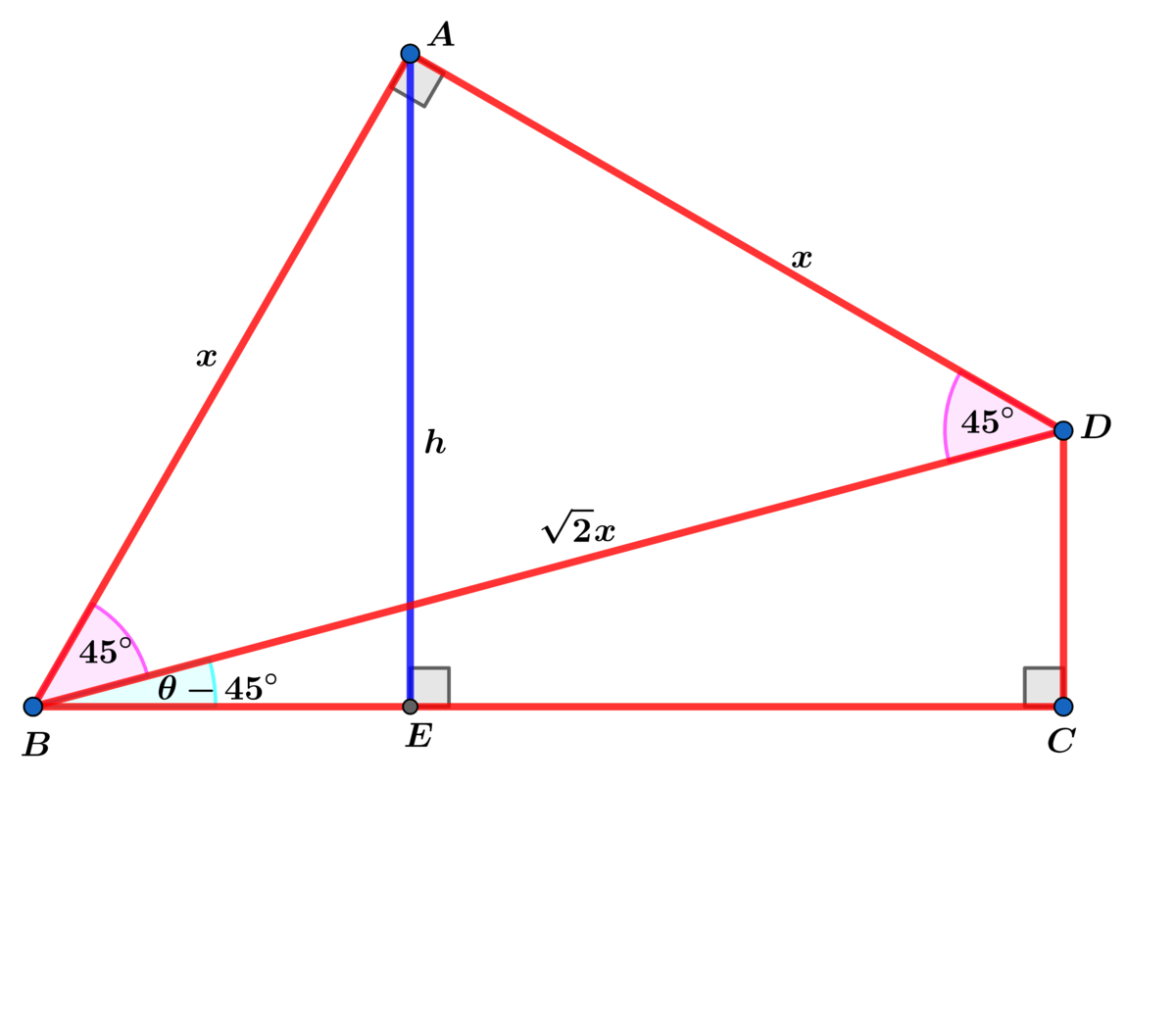
Let m ∠ B = θ and h = B D = x sin ( θ ) .
1 0 0 = A △ A B D + A △ B D C = 2 x 2 + cos ( θ − 4 5 ∘ ) sin ( θ − 4 5 ∘ ) x 2 =
2 x 2 + 2 sin ( 2 θ − 9 0 ∘ ) x 2 ⟹ 2 0 0 = ( 1 − cos ( 2 θ ) ) x 2 = 2 sin 2 ( θ ) x 2 ⟹
1 0 0 = ( x sin ( θ ) ) 2 = h 2 ⟹ h = 1 0 .
How do you know that AB = AD?
Log in to reply
I forgot to type it in the given problem. Thanks, I added it.
It's given.
Log in to reply
It was not given in the original problem but it has since been fixed.
Construct F such that A E C F is a rectangle:
Then ∠ B A E = ∠ B A D − ∠ E A D = 9 0 ° − ∠ E A D = ∠ E A F − ∠ E A D = ∠ D A F , and ∠ B E A = 9 0 ° = ∠ D F A , and since A B = A D , △ B E A ≅ △ D F A by AAS congruency.
Since △ B E A ≅ △ D F A , A A B C D = A A E C F = 1 0 0 . Also since △ B E A ≅ △ D F A , A E = A F , which makes A E C F a square.
As the side of a square with an area of 1 0 0 , A E = 1 0 0 = 1 0 .